SPFA算法详解

前置知识：Bellman-Ford算法

前排提示：SPFA算法非常容易被卡出翔。所以如果不是图中有负权边，尽量使用Dijkstra！（Dijkstra算法不能能处理负权边，但SPFA能）

前排提示*2：一定要先学Bellman-Ford！

0.引子

在Bellman-Ford算法中，每条边都要松弛\(n-1\)轮，还不一定能松弛成功，这实在是太浪费了。能不能想办法改进呢？

非常幸运，SPFA算法能做到这点。（SPFA又名“Bellman-Ford的队列优化”，就是这个原因。）

1.基本思想

先说一个结论：只有一个点在上一轮被松弛成功时，这一轮从这个点连出的点才有可能被成功松弛。

为什么？显而易见

好吧其实我当初也花了不少时间理解这玩意

松弛的本质其实是通过一个点中转来缩短距离（如果你看了前置很容易理解）。所以，如果起点到一个点的距离因为某种原因变小了，从起点到这个距离变小的点连出的点的距离也有可能变小（因为可以通过变小的点中转）。（通读三遍再往下看）

所以，可以在下一轮只用这一轮松弛成功的点进行松弛，这就是SPFA的基本思想。

2.用队列实现

我们知道了在下一轮只用这一轮松弛成功的点进行松弛，就可以把这一轮松弛成功的点放进队列里，下一轮只用从队列里取出的点进行松弛。

为什么是队列而不是其他的玄学数据结构？因为队列具有“先进先出，后进后出”的特点，可以保证这一轮松弛的点不会在这一轮结束之前取出。

干说可能不太理解，所以还是举个栗子吧。

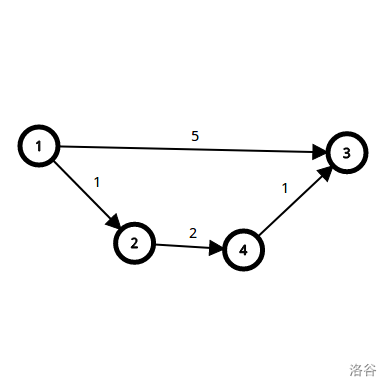
这又是之前的有向图，但是这次我们要用SPFA跑。

最开始，我们要把\(1\)号点放进队列（为什么要这样？先往下看）。\(dis\)数组和队列是这个亚子的：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(\infty\)
\(3\)	\(\infty\)
\(4\)	\(\infty\)

queue	1

用\(1\)号点进行松弛（就是\(1\)号到\(1\)号再到目标点）：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(1\)
\(3\)	\(5\)
\(4\)	\(\infty\)

queue	2	3

\(2,3\)号点被松弛成功了，把它们加入到队列里。

\(1\)号点被用过了，把它扔掉。（工具点石锤）

用\(2\)号点进行松弛：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(1\)
\(3\)	\(5\)
\(4\)	\(3\)

queue	3	4

\(4\)号点被松弛成功了，把它们加入到队列里。

\(2\)号点被用过了，把它扔掉。

用\(3\)号点进行松弛：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(1\)
\(3\)	\(5\)
\(4\)	\(3\)

queue	4

没有点被松弛成功。

\(3\)号点被用过了，把它扔掉。

用\(4\)号点进行松弛：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(1\)
\(3\)	\(4\)
\(4\)	\(3\)

queue	3

\(3\)号点被松弛成功了，把它们加入到队列里。

\(4\)号点被用过了，把它扔掉。

用\(3\)号点进行松弛：

\(i\)	\(dis[i]\)
\(1\)	\(0\)
\(2\)	\(1\)
\(3\)	\(4\)
\(4\)	\(3\)

queue

没有点被松弛成功。

\(3\)号点被用过了，把它扔掉。

现在队列为空（也就是能松弛的都松弛了），算法结束。

3.Code

SPFA的具体实现，推荐结合上面的栗子食用。

#include <bits/stdc++.h>
using namespace std;
#define MAXN 10005
#define INF 0x7fffffff
int n,m,s,dis[MAXN];
vector<pair<int,int> > g[MAXN];//用vector存图，但是据说链式前向星更快
void spfa(){
    queue<int> q;
    q.push(s);//把初始点加入队列
    fill(dis+1,dis+1+n,INF);//因为一开始所有点都到不了，所以初始化为INF
    dis[s]=0;//自己到自己肯定距离为0
    while(!q.empty()){
        int u=q.front();
        q.pop();//从队列里取出第一个元素
        for(int i=0;i<g[u].size();i++){
            int v=g[u][i].first,w=g[u][i].second;
            if(dis[v]>dis[u]+w){
                dis[v]=dis[u]+w;
                q.push(v);
            }
            //如果能松弛成功，那么松弛，把松弛成功的目标点放入队列
        }
    }
}
int main(){
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        g[u].push_back(make_pair(v,w));
    }//输入，建图
    spfa();
    for(int i=1;i<=n;i++){
        printf("%d ",dis[i]);
    }//输出
    return 0;
}

这个代码能够ACP3371，但是我还是推荐你自己码一遍。

4.特点

• 能够处理有负权边的图，但是隔壁Dijkstra不行。
• 在有负环的情况下，不存在最短路，因为不停在负环上绕就能把最短路刷到任意低。但是SPFA能够判断图中是否存在负环，具体方法为统计每个点的入队次数，如果有一个点入队次数$ \ge n $，那么图上存在负环，也就不存在最短路了。
• 什么？你不知道什么叫负环？下面的就是。

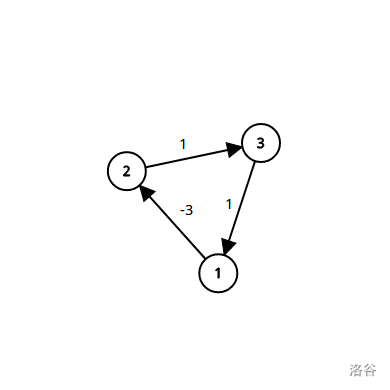
就是一个环，边权和是负。一般用一个名为菜鸡算法的算法判断

——Ynoi

• SPFA的时间复杂度是\(O(km)\)，\(k\)是每一个节点的平均入队次数，经过实践，\(k\)一般为\(4\)，所以SPFA通常情况下非常高效。但是SPFA非常容易被卡出翔，最坏情况下会变成\(O(nm)\)！ 所以如果能用隔壁Dijkstra尽量不要用SPFA。至于具体怎么卡，据说是这样的：

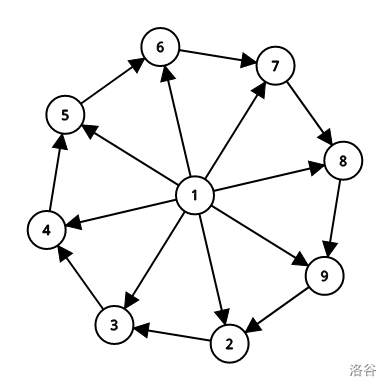
（这种图据说叫菊花图，能欺骗SPFA多次让点进入队列，所以\(k\)会变得非常大（上限为\(n\)）。）

5.你都看到这了就不点一个赞吗？

这个最重要了qwq