FIRST集合、FOLLOW集合及LL(1)文法求法

FIRST集合

定义

可从α推导得到的串的首符号的集合，其中α是任意的文法符号串。

规则

计算文法符号 X 的 FIRST(X)，不断运用以下规则直到没有新终结符号或 ε可以被加入为止 ：

（1）如果 X 是一个终结符号，那么 FIRST(X) = X。

（2）如果 X 是一个非终结符号，且 X ->Y₁ Y₂ … Y_k是一个产生式，其中 k≥1，那么如果对于某个i，a在 FIRST(Y₁）、FIRST(Y₂）… FIRST(Y_i-1）中，就把a加入到 FIRST(X) 中。

（3）如果 X ->ε是一个产生式，那么将ε加入到 FIRST(X)中。

---

以上是书上的官方规则，不仅读起来很拗口，理解也很累。

下面看一下精简版的规则（从别人 @樱草书 那里看来的，感觉很棒，这里引用一下）：

（1）如果X是终结符，则FIRST(X) = { X } 。

（2）如果X是非终结符，且有产生式形如X → a…，则FIRST( X ) = { a }。

（3） 如果X是非终结符，且有产生式形如X → ABCdEF…（A、B、C均属于非终结符且包含 ε，d为终结符），需要把FIRST( A )、FIRST( B )、FIRST( C )、FIRST( d )加入到 FIRST( X ) 中。

（4）如果X经过一步或多步推导出空字符ε，将ε加入FIRST( X )。

实践

记得，曾经有人说过：

只读，就会白给

下面以这个文法为例讲解一波，会用精简版规则，更容易理解一些：

E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id



1
2
3
4
5

1. FIRST(E) = FIRST(T) 根据规则3，很容易理解，这里要注意的由于T不含ε，所以遍历到T就停止了，E’不会加入进来
2. FIRST(E’) = FIRST(+) ∪ FIRST(ε)= { +, ε } 根据规则2和4，,很好理解
3. FIRST(T) = FIRST(F) 根据规则3，和第一条推导过程一样
4. FIRST(T’) = FIRST() ∪ FIRST(ε)= { , ε } 根据规则2和4，和第二条推导一样
5. FIRST(F) = FIRST( ( ) ∪ FIRST(id)= { ( , id } 根据规则2

结果：

FIRST(E) = FIRST(T) = FIRST(F) = { ( , id }
FIRST(E') = FIRST(+) ∪ FIRST(ε)= { + ,  ε }
FIRST(E') = FIRST(*) ∪ FIRST(ε)= { * ,  ε }



1
2
3

FOLLOW集合

定义

对于非终结符号A，FOLLOW（A） 被定义为可能在某些句型中紧跟在A右边的终结符号集合。

规则

计算文法符号 X 的 FOLLOW(X) ，不断运用以下规则直到没有新终结符号可以被加入任意FOLLOW集合为止 ：

（1）将$加入到FOLLOW(X)中，其中S是开始符号，而$是输出右端的结束标记。

（2）如果存在一个产生式S->αXβ，那么将集合FIRST(β)中除ε外的所有元素加入到FOLLOW(X)当中。

（3）如果存在一个产生式 S->αX , 或者S->αXβ且FIRST(β)中包含ε , 那么将集合FOLLOW(S)中的所有元素加入到集合FOLLOW(X)中。

实践

还是用之前的例子来做

E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id



1
2
3
4
5

1. FOLLOW(E) ，根据规则1，首先把$加入进来，根据规则2，可以得出 FOLLOW(E) = { ) , $ }
2. FOLLOW(E’) = FOLLOW(E) = { ) , $ } 根据规则3
3. FOLLOW(T) = FIRST(E’) ∪ FOLLOW(E) = { + , ) , $ } 根据规则2
4. FOLLOW(T’) = FOLLOW(T) = { + , ) , $ } 根据规则3
5. FOLLOW(F) = FOLLOW(T) ∪ FIRST(T’) = { * , + , ) , $ } 根据规则2和3

结果：

FOLLOW(E) = FOLLOW(E') = { ) , $ }
FOLLOW(T) = FOLLOW(T') = { + , ) , $ }
FOLLOW(F) = { * , + , ) , $ }



1
2
3

LL(1)文法

解释

LL(1) 中第一个“L”表示从左向右扫描输入，第二个“L”表示产生最左推导，而“1”表示在每一步中只需要向前看一个输入符号来决定语法分析动作。

定义

对于文法LL(1)文法G，当且仅当G的任意两个不同产生式 A -> α | β

（1）不存在终结符号a使得α和β都能推导出以a开头的串。

（2）α和β中最多只有一个可以推导出空串。

（3）如果 β=》ε ，那么α不能推导出任何以FOLLOW(A)中某个终结符号开头的串。

可能很多人看的云里雾里，解释一下：

（1）和（2）意思是α和β的FIRST集合相交。（3）是指如果FIRST(α)中有 ε，那么FIRST(β)和FOLLOW(A)是不相交的集合，反之一样。

预测分析表的构建

方法：

对于文法G的每个产生式 A->α ，进行如下处理

（1）对于FIRST(α)中每个终结符号a，将 A->α 加入到 M[A,a] 中。

（2）如果 ε在FIRST(α)中，那么对于FOLLOW(A)中每个终结符号b，将 A->α 加入到 M[A,b] 中。如果 ε在FIRST(α)，且$在FOLLOW(A)中，也将 A->α 加入到 M[A,$] 中。

还是以之前的例子示例

E -> T E'
E' -> + T E' | ε
T -> F T'
T' -> * F T' | ε
F -> ( E ) | id



1
2
3
4
5

1.先求FIRST和FOLLOW集合：

FIRST(E) = FIRST(T) = FIRST(F) = { ( , id }
FIRST(E') = FIRST(+) ∪ FIRST(ε)= { + ,  ε }
FIRST(T') = FIRST(*) ∪ FIRST(ε)= { * ,  ε }
FOLLOW(E) = FOLLOW(E') = { ) , $ }
FOLLOW(T) = FOLLOW(T') = { + , ) , $ }
FOLLOW(F) = { * , + , ) , $ }



1
2
3
4
5
6

2.然后构建一个这样的表



3.然后依次填入非终结符号



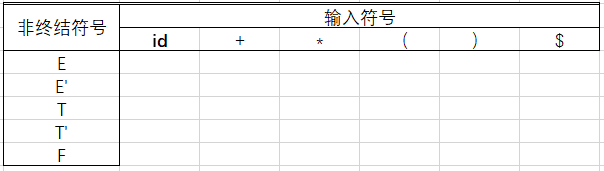
4.按照规则1填写其余内容



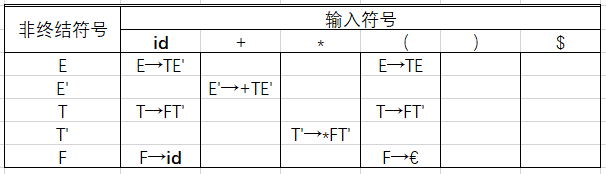
5.按照规则2填写内容



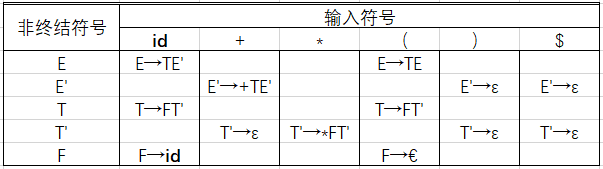
至此整个构建全部完成

                                </div>