AtCoder Beginner Contest 176 E - Bomber (思维)

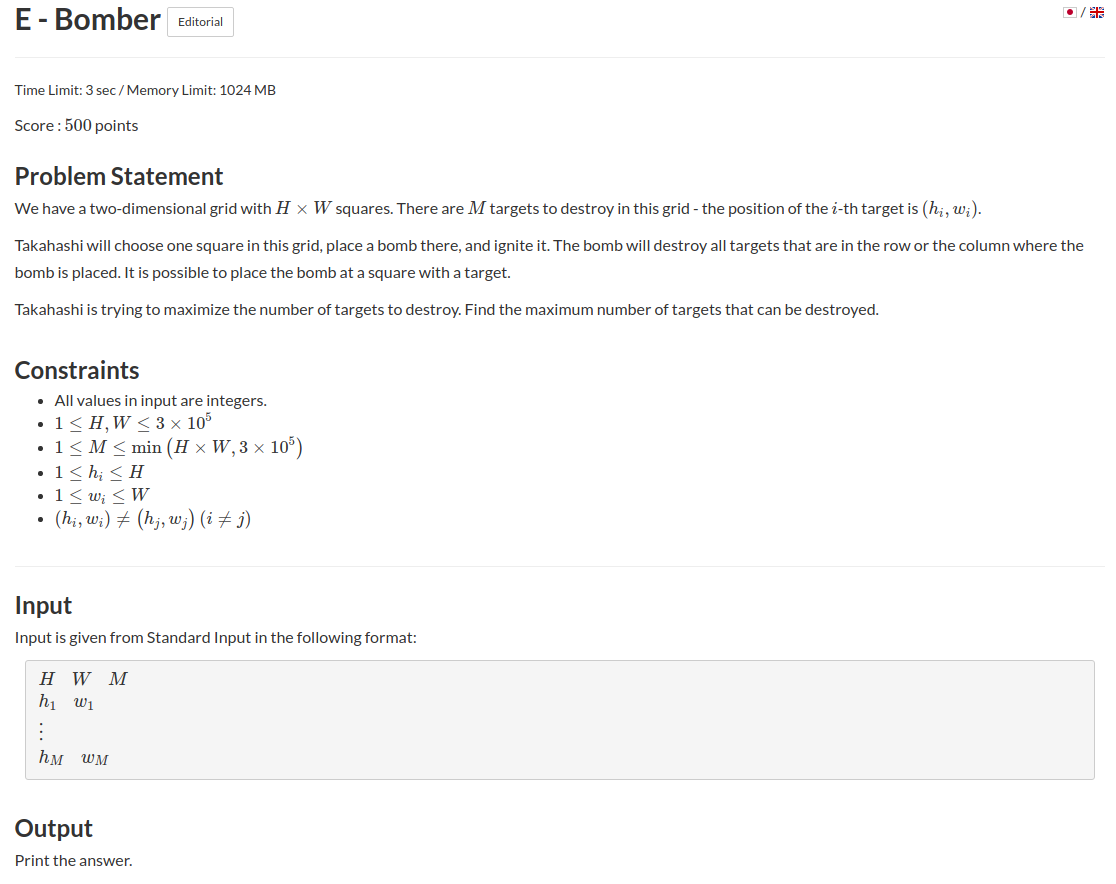
• 题意:有一张\(H\)x\(W\)的图,给你\(M\)个目标的位置,你可以在图中放置一枚炸弹,炸弹可以摧毁所在的那一行和一列,问最多可以摧毁多少目标.

• 题解:首先我们记录某一行和某一列目标最多的数目,用桶标记每个目标的位置,然后记录每一行和每一列的炸弹数,再去枚举每一行和每一列,将目标数等于最大值的存起来,最后再去枚举存起来的拥有最大值的行和列,如果某一行和某一列相交的位置没有目标,那么可以摧毁的最大值就是\(maxr+maxc\)(因为没有重复的点),否则就是\(maxr+maxc-1\)(行和列重复计算了一个,要减去).

• 代码:

  int n,m,w;
  int x,y;
  map<PII,bool> mp;
  vector<int> cnt1,cnt2;
  int row[N],col[N];
  int maxr,maxc;
  
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	n=read();
  	m=read();
  	w=read();
  
  	for(int i=1;i<=w;++i){
  		x=read();
  		y=read();
  
  		mp[{x,y}]=true;
  
  		row[x]++;
  		col[y]++;
  
  		maxr=max(maxr,row[x]);
  		maxc=max(maxc,col[y]);
  	}
  
  	for(int i=1;i<=n;++i){
  		if(row[i]==maxr) cnt1.pb(i);
  	}
  	for(int i=1;i<=m;++i){
  		if(col[i]==maxc) cnt2.pb(i);
    	}
  
    	for(int i=0;i<cnt1.size();++i){
    		for(int j=0;j<cnt2.size();++j){
    			if(!mp[{cnt1[i],cnt2[j]}]){
    				printf("%d\n",maxr+maxc);
    				return 0;
    			}
    		}
    	}
  
    	printf("%d\n",maxr+maxc-1);
  
      return 0;
  }