P2764 最小路径覆盖问题 题解（二分图）

建图思路很明确，拆点跑最大匹配，但这明显是个二分图的题题解居然只有一篇匈牙利算法。

发一种和之前那篇匈牙利思路略有不同的题解。

本题的难点就是如何输出，那么我们不妨在建图的时候加入一个原则，即：连边时位于左图的顶点编号小于位于右图的。

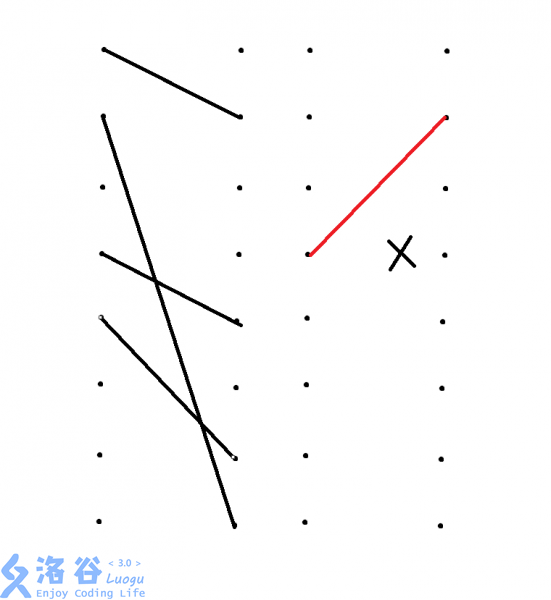
也就是说，形如左图的边是允许的，而形如右图的边是不允许的。

这很好理解吧~

在输出的时候，只要不停往上找即可。

上代码

#include<stdio.h>
int n,m,e[200][200],vis[200],mt[200],p[200];
int dfs(int p,int t){
	int i;
	for(i=p;i<=n;i++){//从p开始找右半边匹配
		if(e[p][i]&&vis[i]!=t){
			vis[i]=t;
			if(!mt[i]||dfs(mt[i],t))return mt[i]=p;
		}
	}
	return 0;
}
int maxflow(){
	int i,ans=0;
	for(i=1;i<=n;i++)if(dfs(i,i))ans++;
	return ans;
}
int main(){
	int i,a,b,x;
	scanf("%d%d",&n,&m);
	for(i=0;i<m;i++){
		scanf("%d%d",&a,&b);
		if(a>b){int t=a;a=b;b=t;}//保证a<b
		e[a][b]=1;
	}
	int ans=maxflow();
	for(i=n;i;i--)if(!p[i]){
		x=i;
		do{
			printf("%d ",x);
			x=mt[x];p[x]=1;//p[i]表示已输出
		}while(x);
		printf("\n");
	}
	printf("%d",n-ans);
	return 0;
}