Python 实现图像快速傅里叶变换和离散余弦变换

图像的正交变换在数字图像的处理与分析中起着很重要的作用，被广泛应用于图像增强、去噪、压缩编码等众多领域。本文手工实现了二维离散傅里叶变换和二维离散余弦变换算法，并在多个图像样本上进行测试，以探究二者的变换效果。

1. 傅里叶变换

实验原理

对一幅图像进行离散傅里叶变换（DFT），可以得到图像信号的傅里叶频谱。二维 DFT 的变换及逆变换公式如下：

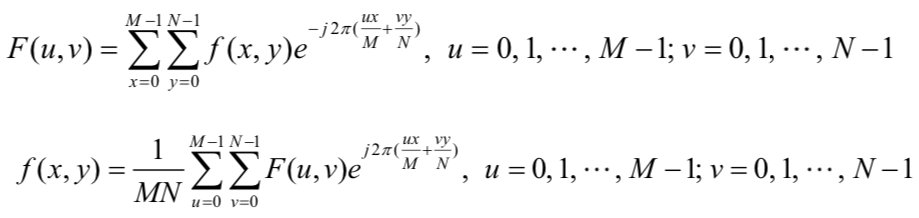
DFT 尽管解决了频域离散化的问题，但运算量太大。从公式中可以看到，有两个嵌套的求和符号，显然直接计算的复杂度为 \(O(n^2)\) 。为了加快傅里叶变换的运算速度，后人提出快速傅里叶变换（FFT），即蝶形算法，将计算 DFT 的复杂度降低到了 \(O(n\log n)\)。

FFT 利用傅里叶变换的数学性质，采用分治的思想，将一个 \(N\) 点的 FFT，变成两个 \(N/2\) 点的 FFT。以一维 FFT 为例，可以表示如下：

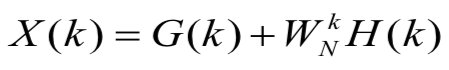
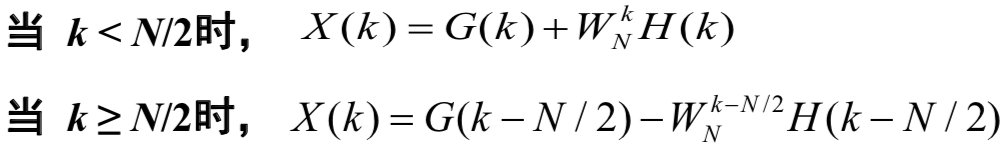
其中，\(G(k)\) 是 \(x(k)\) 的偶数点的 \(N/2\) 点的 FFT，\(H(k)\) 是 \(x(k)\) 的奇数点的 \(N/2\) 点的 FFT。

这样，通过将原问题不断分解为两个一半规模的子问题，然后计算相应的蝶形运算单元，最终得以完成整个 FFT。

算法步骤

本次实验中，一维 FFT 采用递归实现，且仅支持长度为 2 的整数幂的情况。

算法步骤如下：

检查图像的尺寸，如果不是 2 的整数幂则直接退出。
对图像的灰度值进行归一化。
对图像的每一行执行一维 FFT，并保存为中间结果。
对上一步结果中的每一列执行一维 FFT，返回变换结果。
将零频分量移到频谱中心，并求绝对值进行可视化。
对中心化后的结果进行对数变换，以改善视觉效果。

主要代码

一维 FFT

def fft(x):

    n = len(x)

    if n == 2:

        return [x[0] + x[1], x[0] - x[1]]

    G = fft(x[::2])

    H = fft(x[1::2])

    W = np.exp(-2j * np.pi * np.arange(n//2) / n)

    WH = W * H

    X = np.concatenate([G + WH, G - WH])

    return X

二维 FFT

def fft2(img):

    h, w = img.shape

    if ((h-1) & h) or ((w-1) & w):

        print('Image size not a power of 2')

        return img

    img = normalize(img)

    res = np.zeros([h, w], 'complex128')

    for i in range(h):

        res[i, :] = fft(img[i, :])

    for j in range(w):

        res[:, j] = fft(res[:, j])

    return res

零频分量中心化

def fftshift(img):

    # swap the first and third quadrants, and the second and fourth quadrants

    h, w = img.shape

    h_mid, w_mid = h//2, w//2

    res = np.zeros([h, w], 'complex128')

    res[:h_mid, :w_mid] = img[h_mid:, w_mid:]

    res[:h_mid, w_mid:] = img[h_mid:, :w_mid]

    res[h_mid:, :w_mid] = img[:h_mid, w_mid:]

    res[h_mid:, w_mid:] = img[:h_mid, :w_mid]

    return res

运行结果

2. 余弦变换

实验原理

当一个函数为偶函数时，其傅立叶变换的虚部为零，因而不需要计算，只计算余弦项变换，这就是余弦变换。离散余弦变换（DCT）的变换核为实数的余弦函数，因而计算速度比变换核为指数的 DFT 要快得多。

一维离散余弦变换与离散傅里叶变换具有相似性，对离散傅里叶变换进行下式的修改：

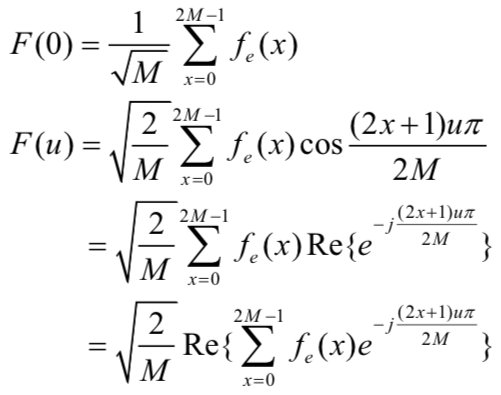
式中

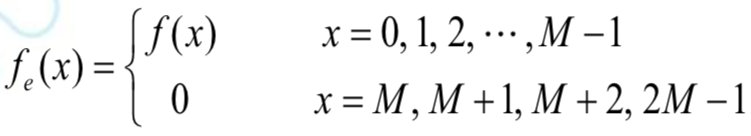
由上式可见，\(\sum\limits_{x=0}^{2M-1}f_e(x)e^{\frac{-j2ux\pi}{2M}}\) 是 \(2M\) 个点的傅里叶变换，因此在做离散余弦变换时，可将其拓展为 \(2M\) 个点，然后对其做离散傅里叶变换，取傅里叶变换的实部就是所要的离散余弦变换。

算法步骤

基于上述原理，二维 DCT 的实现重用了上文中的一维 FFT 函数，并根据公式做了一些修改。

算法步骤如下：

检查图像的尺寸，如果不是 2 的整数幂则直接退出。
对图像的灰度值进行归一化。
对图像的每一行进行延拓，执行一维 FFT 后取实部，乘以公式中的系数，并保存为中间结果。
对上一步结果中的每一列进行延拓，执行一维 FFT 后取实部，乘以公式中的系数，返回变换结果。
对结果求绝对值，并进行对数变换，以改善视觉效果。

主要代码

二维 DCT

def dct2(img):

    h, w = img.shape

    if ((h-1) & h) or ((w-1) & w):

        print('Image size not a power of 2')

        return img

    img = normalize(img)

    res = np.zeros([h, w], 'complex128')

    for i in range(h):

        res[i, :] = fft(np.concatenate([img[i, :], np.zeros(w)]))[:w]

        res[i, :] = np.real(res[i, :]) * np.sqrt(2 / w)

        res[i, 0] /= np.sqrt(2)

    for j in range(w):

        res[:, j] = fft(np.concatenate([res[:, j], np.zeros(h)]))[:h]

        res[:, j] = np.real(res[:, j]) * np.sqrt(2 / h)

        res[0, j] /= np.sqrt(2)

    return res

运行结果

完整源码请见 GitHub 仓库