SPSS基础学习方差分析—单因素分析

为什么要进行方差分析？

• 单样本、两样本t检验其最终目的都是分析两组数据间是否存在显著性差异，但如果要分析多组数据间是否存在显著性差异就很困难，因此用方差分析解决这个问题；
  举例：t检验可以分析一个班男女的入学成绩差异；而方差分析可以分析一个班来自各省市地区同学的入学成绩。
• 在方差分析中，涉及到控制变量和随机变量以及观测变量；
  举例：施肥量是否会给农作物产量带来显著影响；这里，控制变量：施肥量，观测变量：农作物产量，随机变量：天气、温度……

单因素分析

目的：分析单一控制因素影响下的多组样本的均值是否存在显著性差异。

适用条件：

• 正态性，每个水平下的因变量应服从正态分布；
• 同方差性，各组之间的具有相同的方差；
• 独立性，各组之间是相互独立的。

案例分析：

案例描述：在某一公司下，分析广告形式对销售额的影响。（数据来源：《统计分析与SPSS的应用》（第五版）薛薇 第六章）

题目分析：在题目中，广告形式不至两种，没办法用两独立样本t检验分析形式和销售额之间的显著性差异，同时，只有一个控制因素，所以采用方差分析中的单因素分析。

提出原假设：广告形式和销售额之间不存在显著性差异。

界面操作步骤：分析—比较均值—单因素ANOVA

关键步骤截图：

分清楚因变量列表和因子；因子：控制变量，因变量列表：观测变量

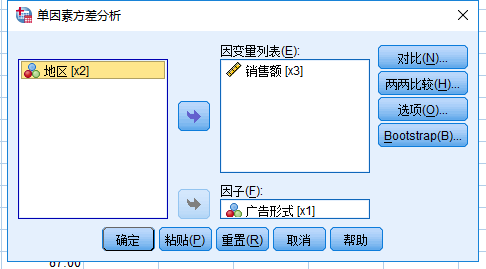
结果分析：

单因素方差分析
销售额
	平方和	df	均方	F	显著性
组间	5866.083	3	1955.361	13.483	.000
组内	20303.222	140	145.023
总数	26169.306	143

 

分析：

• 平方和：组间离差平方和（SSA）是由控制变量的不同水平造成的变差，组内离差平方和（SSE）是由随机变量的不同水平造成的变差；
• df：组间自由度，在本题中根据广告形式的不同分为四组，所以自由度为k-1=4-1=3;组内自由度n-k=144-k=140;
• 均方：即为方差；
• F=SSA/(k-1)÷（SSE/(n-k)）=组间方差/组内方差，F值显著性大于1，说明控制变量对观测变量的影响比随机变量大，反之有效；
• P-值=0.00<0.05，所以拒绝原假设，认为不同的广告形式和地区对销售额的平均值产生了显著影响，不同的广告形式、地区对销售额的影响效应不全为0。

单因素进一步检验分析：

方差齐性检验：在上述描述中提到，满足单一因素分析的条件是各组别的方差要相同，所以需要方差齐性检验；

思路：

1. 提出原假设：各组别的方差不存在显著差异；
2. 利用Levene F方法间行检验；
3. 将p值与ɑ进行比较，判断各组之间方差是否相同。

用上述题目继续分析：

首先，假设不同的广告形式总体的方差相同；

在如同上述截图得界面中点击“选项”，得到如图：

选择方差同质性检验

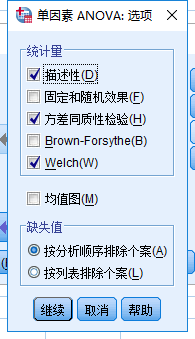
结果分析：

描述
销售额
	N	均值	标准差	标准误	均值的 95% 置信区间		极小值	极大值
					下限	上限
报纸	36	73.2222	9.73392	1.62232	69.9287	76.5157	54.00	94.00
广播	36	70.8889	12.96760	2.16127	66.5013	75.2765	33.00	100.00
宣传品	36	56.5556	11.61881	1.93647	52.6243	60.4868	33.00	86.00
体验	36	66.6111	13.49768	2.24961	62.0442	71.1781	37.00	87.00
总数	144	66.8194	13.52783	1.12732	64.5911	69.0478	33.00	100.00

方差齐性检验
销售额
Levene 统计量	df1	df2	显著性
.765	3	140	.515

 分析：广告形式有四种：报纸，广播，宣传品以及体验，现在需要对这四组的方差进行判断，看到第二个图，我们可以看到显著性0.515>ɑ，所以接受假设，因此这四组的方差相同，符合单因素分析的条件。

参考书籍：

《SPSS统计分析从零开始》吴骏

《SPSS统计分析基础教程》张文彤

《统计分析与SPSS的应用》（第五版）薛薇