论文学习-wlg-基于二维材料的肖特基异质结构的通用尺度定律

目录

• 主要公式：
  • 各个段落的内容
    • 第一页
    • 第二页
    • 第三页
  • 名词的含义
    • 功函数：
    • 电子亲和力
    • 肖特基势垒
    • 肖特基二极管的原理
    • 非相对论性电子气：未知
    • Rashba自旋电子系统：
  • 参考链接：

主要公式：

证明了经典方程中B=2 是错误的；

意义：基于2D材料的异质结构中肖特基势垒高度的提取提供简单的分析标度

各个段落的内容

第一页

第一段：我们主要研究二维结构的肖特基势垒；

第二段：结电压V，电流密度J（rsc），方程表示：

广义的公式表示

AB依赖于表面材料， B等于2是传统3D的，方程1，和已经知道的B=2，简化了提取SBH；SBH的提取很关键；

第三段：2D的SBH提取依旧关键；

受到很多因素影响；

石墨烯基肖特基的能带图

异质结构显示肖特基上的热电子传输屏障，基于石墨烯的示意图2D / 3D横向肖特基异质结构

第二页

第一段：为什么要研究；SBH数据智慧h不同β 值存在混淆性并存；仍然缺失基于2d的横向， 垂直的

第二段：分三点说了发现的详细结论：

1. 对于多种系统，LSH中，电流标度指数B=3/2;
2. VSH中，B=1;缺乏通用性；
3. B=2是错误的；

第三段：给出了详细的公式推导， 2到七个公式： 2D结构中，RSC公式的表示：

2D材料，

不需要考虑电流温度关系，（3）可变换为（4）：

从（3）中提取温度，可变成

结合（2）（5）以及这个条件，、

，泰勒展开，可以得到公式（6）

第三页

B=3/2在各个系统中，反向饱和电流的表示：拿石墨烯定量评估， B=3/2在LSH，B=1 在VLS，比传统的B=2更加的拟合；

名词的含义

垂直肖特基异质结构（VSH

横向肖特基异质结构（LSH）

SBH：肖特基势垒高度

RSC：反向饱和电流密度；J

功函数：

表示要让电子从材料中逃逸到自由空间中的最小热能量，

电子亲和力

表示电子从自由空间掉落到半导体导带底部所释放的能量。

肖特基势垒

而当两种材料接触时，载流子扩散流动必须使接触面两侧的费米能级相等才能达到平衡状态。所以接触后半导体中的能带会因内建电场而弯曲，如下图：

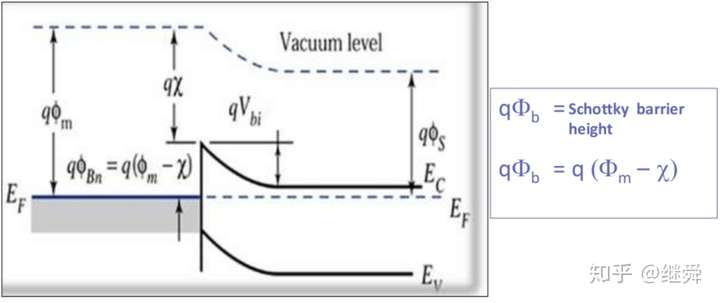
这样就在接触面形成了电子的势垒，称为肖特基势垒(schottky barrier)。形成整流节(rectifying junction)。肖特基二极管就是利用该原理工作的。

肖特基二极管的原理

肖特基二极管又名点接触二极管，它与 PN 二极管具有类似的整流特性。一般出现在 n 型半导体中，是由 Wm Ws 的金属与半导体接触而成。 在 Wm Ws 时，当导带底电子向金属运动时必须越过的势垒的高度为 qVD=Wm-Ws，金 属一侧的电子运动到半导体一侧也需要越过的势垒高度为 在势垒区足够薄， 以至半导体中处于势垒边缘的能量足够高的电子能够不经碰撞地进入到金属中，这时，对其 电学特性起决定作用的是势垒高度。正偏下，半导体一侧的势垒高度随着偏压的增加而减少， 所以电压增加会使得电流增加。反偏下，半导体一侧的势垒高度随着偏压的增加而变高，而 金属一侧的势垒高度不变；在偏压很小时，只有极少量的电子会通过热运动的方式越过半导 体一侧的势垒进入金属，而在外电场作用下，电子是从金属流向半导体，所以电压增加会使 得电流（电流绝对值）略有增加；当电压值足够大（电压绝对值）时，主电流来自于从金属 流向半导体的电子，由于金属一侧的势垒高度不变，所以形成反向饱和电流。这就是肖特基 二极管的整流特性。 半导体内部的电子只要有足够的能量超越半导体一侧势垒的顶点，就可以自由地通过阻 挡层进入金属。同样，金属中能超越金属一侧势垒顶的电子也都能到达半导体内。对于 Ge、 Si、GaAs 之类的半导体，由于具有较高的载流子迁移率，载流子的平均自由程较大，在室温 下，其肖特基势垒中的电流输运机构主要是多数载流子的热电子发射。所以，电流的计算归 结为热电子发射理论

非相对论性电子气：未知

Rashba自旋电子系统：

打破空间对称性有两类方法，分别对应了Rashba类型和Dressalhauss类型的自旋轨道耦合项：

类型1（Rashba）. 加电场或者生成异质结（heterostructure）。Rashba项存在于单轴（uniaxial)晶体或2维材料中；

参考链接：

https://www.researchgate.net/publication/323571093_Universal_Scaling_Laws_in_Schottky_Heterostructures_Based_on_Two-Dimensional_Materials