【BZOJ4237】 稻草人 CDQ分治+单调栈

题目描述

---

JOI村有一片荒地，上面竖着N个稻草人，村民们每年多次在稻草人们的周围举行祭典。

有一次，JOI村的村长听到了稻草人们的启示，计划在荒地中开垦一片田地。和启示中的一样，田地需要满足以下条件：

田地的形状是边平行于坐标轴的长方形；

左下角和右上角各有一个稻草人；

田地的内部(不包括边界)没有稻草人。

给出每个稻草人的坐标，请你求出有多少遵从启示的田地的个数

简述 求\(n\)个点组成的内部不含其它点的矩形有多少

Solution

为什么要专门记录这个简单的\(CDQ\)分治+单调栈简单题呢,那是因为这道题脱离了\(CDQ\)分治的模板，转更深刻的探究\(CDQ\)分治解决的问题本质

首先这道题找矩形，就要找其左下角及右上角

我们把被处在右上角的点\(b\)与左下角的点\(a\)形成有效矩形成称为\(b\)控制\(a\)

可理解为，处在左下位置的点会对右上位置的点造成贡献，被控制

我们把点按\(y\)轴排序

按\(y\)来划分上下

上下以\(x\)来归并排序(结果就是,\([ql,mid]\)的\(y\)都比\([mid+1,qr]\)的\(y\)要小,但区间内有且仅有\(x\)有序)

如图，\([ql,mid]\)为上面,\([mid+1,qr]\)为下面

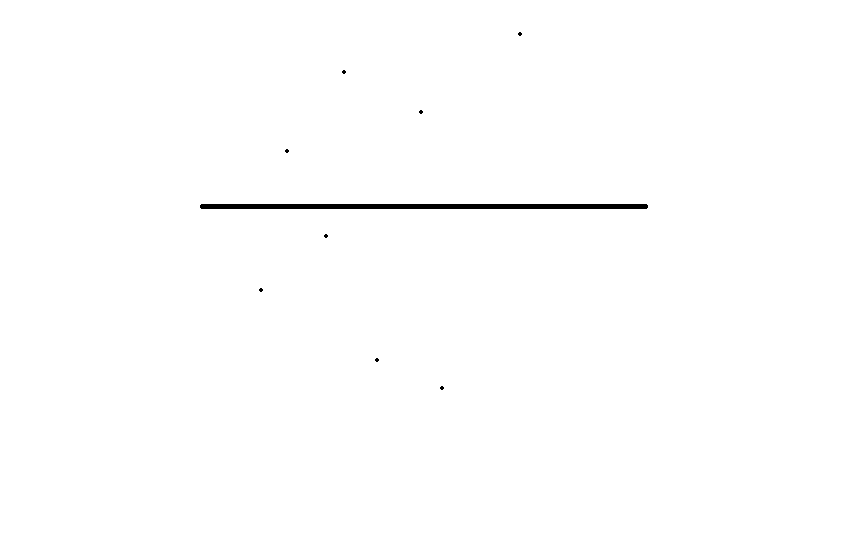
因此\(a\)来自下方,\(b\)来自上方

\(Ans_b\)=(在\(b\)左侧可以成为左下角的\(a\)-被\(b\)左边的管并且不会被\(b\)管的\(a\))

对在\(b\)左侧可以成左下角的\(a\)

现在证明:如果\(a\)是满足条件的，则在\(a\)右上侧的\(a'\)就是无效的

分两种情况

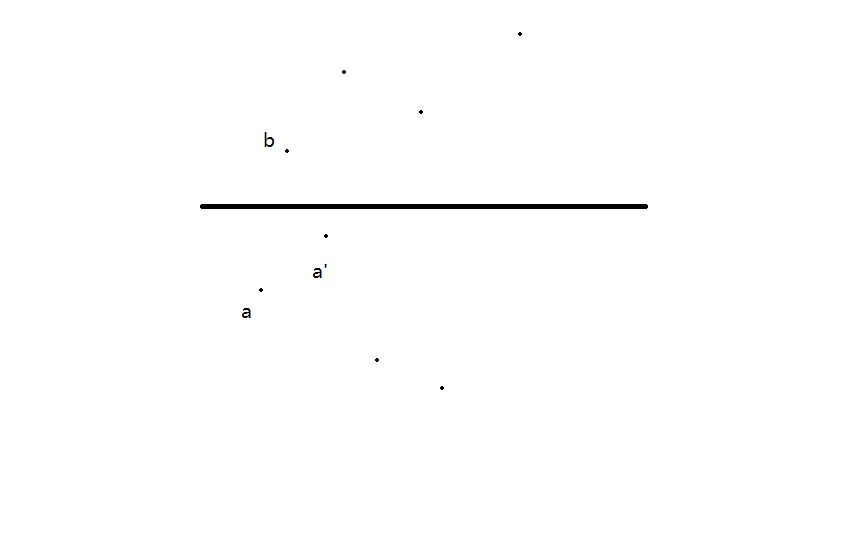
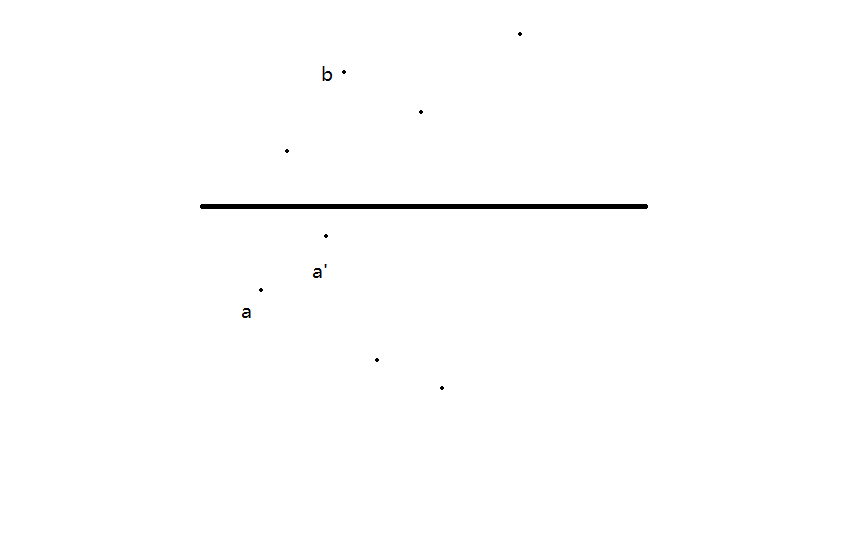
因此对\(a\)我们维护一个\(y\)值单调递减的单调栈

每次维护\(x<b_x\)的单调栈即可

for(;q[j].x<q[i].x&&j<=mid;++j){//下,保存的是所有可以成为左下角的点
			while(topmax&&q[j].y>q[stmax[topmax]].y)--topmax;
			stmax[++topmax]=j;
		}

被\(b\)左边的管并且不会被\(b\)管的\(a\)

现在证明:在\(b\)左下侧的\(b'\)是不会影响\(b\)管辖范围的

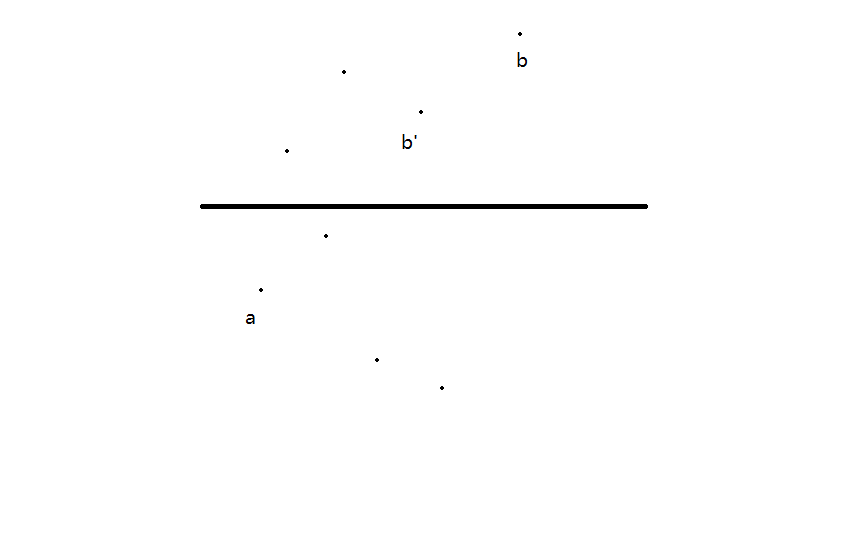
因此对\(b\)我们维护一个\(y\)值单调递增的单调栈

每一次

\(Ans_b\)=(在\(b\)左侧可以成为左下角的\(a\)-被\(b\)左边的管并且不会被\(b\)管的\(a\))

=\(topmax-b\)的单调栈的前栈顶管辖的\(a\)个数

实现时用二分即可找到前栈顶管辖的最后一个\(a\)位置减掉即可

inline int Find(void){
	re int l=1,r=topmax,mid,ans=0;
	while(l<=r){
		mid=(l+r)>>1;
		if(q[stmax[mid]].x<q[stmin[topmin-1]].x){ans=mid;l=mid+1;}
		else r=mid-1;
	}
	return ans;
}
inline void CDQ(re int ql,re int qr){
	re int i,j,l,r,t,mid=(ql+qr)>>1;
	if(ql==qr)return ;
	CDQ(ql,mid);CDQ(mid+1,qr);
	j=ql;topmin=topmax=0;
	for(i=mid+1;i<=qr;++i){//上,保存的是所有可以影响之后右上角点的(左下角点的个数)的点
		while(topmin&&q[i].y<q[stmin[topmin]].y)--topmin;
		stmin[++topmin]=i;
		for(;q[j].x<q[i].x&&j<=mid;++j){//下,保存的是所有可以成为左下角的点
			while(topmax&&q[j].y>q[stmax[topmax]].y)--topmax;
			stmax[++topmax]=j;
		}
		ans+=topmax-Find();
	}
	l=t=ql;r=mid+1;
	while(l<=mid&&r<=qr){
		if(q[l].x<q[r].x)tmp[t++]=q[l++];
		else tmp[t++]=q[r++];
	}
	while(l<=mid)tmp[t++]=q[l++];
	while(r<=qr)tmp[t++]=q[r++];
	for(i=ql;i<=qr;++i)q[i]=tmp[i];
}

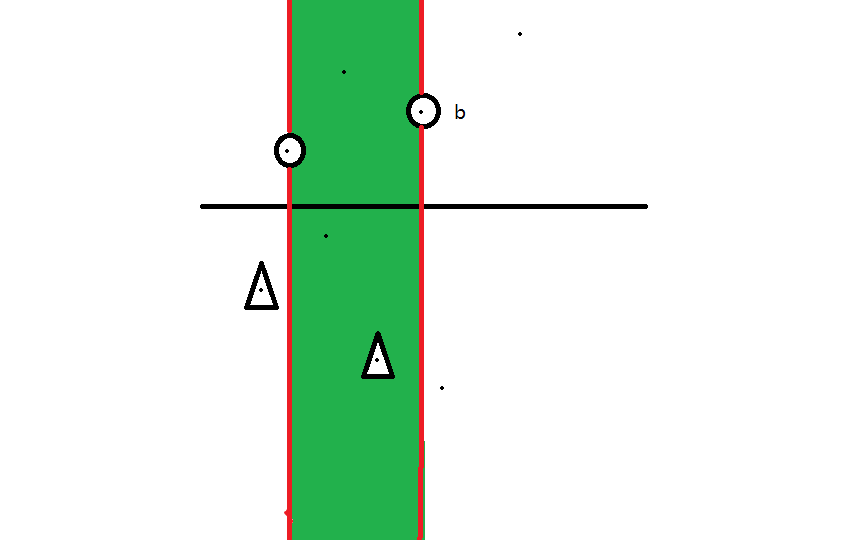
放一个示意图(一定要手推)