P1983 车站分级[拓扑]

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n1,2,…,n的 nn个火车站。每个火车站都有一个级别，最低为 11 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 xx，则始发站、终点站之间所有级别大于等于火车站xx 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是55趟车次的运行情况。其中，前44 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（2级）却未停靠途经的 6号火车站（亦为 2 级）而不满足要求。

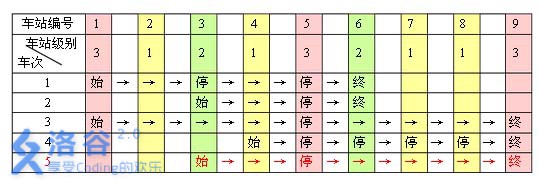
现有 mm 趟车次的运行情况（全部满足要求），试推算这nn 个火车站至少分为几个不同的级别。

解析

这题蛮好的，有助于更深入理解图论（可能吧），更有助于锻炼思维，如果可以的话，希望各位在独立思考出解法之前，能够多思考一下，反正我自己是想了一晚上。

---

首先分析题目，应该能很快发现每条线路对最终答案造成的影响。即，对于任意一条合法线路，其没有停靠的车站的等级恒小于其停靠过的车站的等级。

讲讲我的思路历程吧：

首先想到一种贪心，我们知道某条线路未停靠的点越少，其对最终答案的影响越小，但是经过尝试会发现这种贪心是有后效性的，不可行。

继而把思路引到图论上，图论的一个极其重要的作用大概就是维护一些抽象的关系以及限制条件，具体而明显地，比如并查集、网络流、差分约束等，其建模的本质是依靠题目中隐含的对象之间的某种关系。

那么这样想的话这题思路还是比较明显的，上面也提到过对于一条线路，其没有停靠的车站的等级恒小于其停靠过的车站的等级。这就是我们需要维护的关系。

这就很容易联想到拓扑排序，其维护的正是这种优先级大小关系。意即DAG中每一拓扑序的节点其等级大小是一致的。

我们感性地理解一下，题目告诉我们数据全部是满足要求的，实际上也就是告诉我们如果按照上面的思路建图，建出来必定是一个DAG（车站大小关系一定不会出现矛盾）。

题目要求最少划分的级别数，那我们只用使相邻拓扑序之间的节点等级差都只为1就可以了。

具体做法就是对于所有数据由等级小的车站向等级大的车站连有向边，再做一个拓扑排序就行了。

参考代码

代码略丑，实现比较简陋，如有疏漏望各位巨佬指出不足！

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 1010
#define MOD 2520
#define E 1e-12
using namespace std;
inline int read()
{
	int f=1,x=0;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
vector<int> g[N];
int head[N],tot,n,m,ing[N],dat[N][N],c[N];
bool v[N][N];
int main()
{
	n=read(),m=read();
	for(int i=1;i<=m;++i){
		int s=read();dat[i][0]=s;
		for(int j=1;j<=s;++j) dat[i][j]=read();//读入数据
	}
	for(int i=1;i<=m;++i){
		int now=dat[i][1]+1;
		for(int j=2;j<=dat[i][0];++j){
			while(now<dat[i][j]){
				for(int k=1;k<=dat[i][0];++k)
                //维护节点之间大小关系
					if(!v[now][dat[i][k]]) g[now].push_back(dat[i][k]),ing[dat[i][k]]++,v[now][dat[i][k]]=1;
				now++;
                //注意及时排除已经确定的关系，否则会T
			}
			now++;
		}
	}
	int ans=0;
	queue<int> q;
	for(int i=1;i<=n;++i)//拓扑排序
		if(ing[i]==0) q.push(i),c[i]=1;
	while(q.size()){
		int x=q.front();q.pop();
		for(int i=0;i<g[x].size();++i){
			int y=g[x][i];
			if(--ing[y]==0) c[y]=c[x]+1,ans=max(ans,c[y]),q.push(y);
		}
	}
	cout<<ans<<endl;
	return 0;
}

写完这题的一点个人感想

对于图论，很多看似无法用图论去做的题，实际上隐藏了许多暗示，可以用图论去维护某些信息，进而求解。个人认为，图论是一个下限很低但是上限挺高的一门学问，其蕴含的骚操作还是很多的。