Bagging 和RF的区别

跑训练无聊看了看别人的面经，发现自己一时半会答不上来，整理一下。

一、Bagging介绍

　　先看一个Bagging的一个概念图(图来自https://www.cnblogs.com/nickchen121/p/11214797.html)

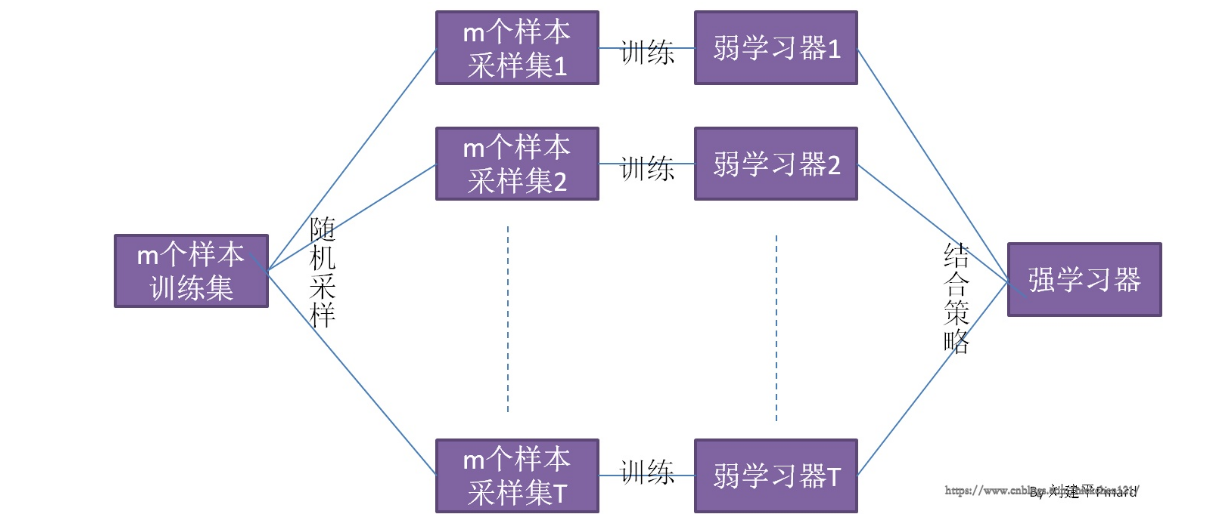
　　从上图可以看出，Bagging的弱学习器之间的确没有boosting那样的联系。它的特点在“随机采样”。那么什么是随机采样？随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本，但是每采集一个样本后，都将样本放回。也就是说，之前采集到的样本在放回后有可能继续被采集到。　　对于我们的Bagging算法，一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同，但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样，则由于随机性，T个采样集各不相同。　　

　　注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样，而Bagging的子采样是放回采样。对于一个样本，它在某一次含m个样本的训练集的随机采样中，每次被采集到的概率是$\frac{1}{m}$。不被采集到的概率为$1-(\frac{1}{m})$。如果m次采样都没有被采集中的概率是$(1-\frac{1}{m})^m$.当m趋近于无穷的时候,$(1-\frac{1}{m})^m$趋近于$\frac{1}{e}$。也就是说，在bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采样集采集中。对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合因此可以用来检测模型的泛化能力。Bagging算法流程如下所示：

　　

二、 RF介绍

理解了Bagging算法自然就好理解RF了。 RF是Bagging的一个改进，它的思想仍然是bagging,但是进行了独有的改进。首先，RF选择CART作为弱学习器（这点和GBRT类似），其次RF对决策树做了改进，对于普通的决策树，我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分，但是RF通过随机选择节点上的一部分样本特征，这个数字小于n，记作$n_{sub}$。然后在这些随机选择的$n_{sub}$中选择一个最优的特征来做决策树的左右子树叶划分。这样进一步增强了模型的泛化能力。如果$n_{sub}$越小，则此时的RF的CART决策树和普通的CART决策树没有什么区别。$n_{sub}$越小，RF越鲁棒，对应的其拟合的程度会变差，对应的方差小，bias偏大。实际的使用过程中就需要用CV来选择一个合适的值。

（Bagging和RF主要的区别应该是RF使用的是CART，且RF对CART划分的规则上做了一些修改，不是对所有属性选择最优，而是随机选取一部分属性，然后从这部分属性中选最优）