canvas教程(三) 绘制曲线

经过 canvas 教程(二) 绘制直线 我们知道了 canvas 的直线是怎么绘制的

而本次是给大家带来曲线相关的绘制

绘制圆形

在 canvas 中我们可以使用 arc 方法画一个圆

context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();

我们是第一次用到 beginPath 和 closePath 这两个方法，首先这两个方法故名思意就是开始路径和结束路径，一般都是配合使用的。

对于 arc 的方法的参数，x 和 y 代表的是圆心的坐标，r 是指圆的半径，startRadian 和 endRadian 是指开始的角度和结束的角度

注意：这里是以弧度为单位的！

1π 等于 180 度，所以我们这里写的时候一般是写成 度数*Math.PI/180，方便我们一眼看出度数是多少

而 antclockwise 是指是否是逆时针绘制，默认是 false

有朋友会说了，我试了一下，写了这三句没有效果啊，怎么回事？没有效果是肯定的，因为这三句仅仅只是描述了一个路径！并没有绘制！所以我们可以用上绘制直线中使用的“描边”stroke 或者“填充”fill

描边三角形：

context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();
context.strokeStyle = '颜色值';
context.stroke();
//描边 填充fill 同理  就不写了

绘制弧线

弧线是圆的一部分，那么如何绘制一个弧度呢，有朋友就发现了我们刚才的 arc 也有一个弧度，

只是两个弧度之间的点有连接的一条直线，那么我去掉直线是不是就是弧线了呢？宾果！就是这样，只要你去掉 closePath 就会发现你画了一条弧线了 2333

好了那么 canvas 其实还有一个画弧线的方法 arcTo(x1,y1,x2,y2,radius);

我们要通过 arcTo 画一条弧线，需要提供三个点的坐标，开始点一般是通过 moveTo 和 lineTo 提供

x1 和 y1 是控制点，x2 和 y2 是结束点，radius 则是圆弧的半径

arcTo()方法将利用当前端点、端点 1(x1,y1)和端点 2(x2,y2)这三个点所形成的夹角

然后绘制一段与夹角的两边相切并且半径为 radius 的圆上的弧线

弧线的起点就是当前端点所在边与圆的切点

弧线的终点就是端点 2(x2,y2)所在边与圆的切点，并且绘制的弧线是两个切点之间长度最短的那个圆弧。

如果当前端点不是弧线起点，arcTo()方法还将添加一条当前端点到弧线起点的直线线段。

我画一个图：

咳咳，别介意画工，大概就是这样的，开始点是我们的当前的点就是使用 arcTo 之前的点

下面我写两段代码演示一下起点一致和起点不一致的情况

    context.moveTo(50, 50);
    context.lineTo(150, 50);
    ctx.arcTo(200,50, 200,100, 50);
    ctx.stroke();

    context.moveTo(50, 50);
    ctx.arcTo(200,50, 200,100, 50);
    ctx.stroke();

是不是发现结果是一样的！

其中区别就细细品味吧，数学知识可以补一补

绘制贝塞尔曲线

百度百科：贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。

更多的就大家自行搜索吧，由于一次贝塞尔曲线就是直线，这里就不讲了，我们直接讲 canvas 如何绘制二次贝塞尔曲线

二次贝塞尔曲线

cnavas 提供了一个方法 quadraticCurveTo(x1,y1,x2,y2)， 其中参数 x1 和 y1 是控制点，x2 和 y2 是结束点

起始点是调用方法之前的点

动图我不会画，但是我之前网上找到一个:

context.strokeStyle = 'red';
context.beginPath();
context.moveTo(0, 150);
context.quadraticCurveTo(75, 50, 200, 100);
context.stroke();
context.strokeStyle = 'green';
context.beginPath();
context.moveTo(75, 50);
context.lineTo(0, 150);
context.moveTo(75, 50);
context.lineTo(200, 100);
context.stroke();

代码效果:

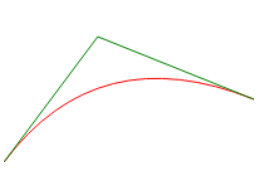
三次贝塞尔曲线

三次贝塞尔曲线的方法则是 bezierCurveTo(x1,y1,x2,y2,x3,y3)

其中参数 x1、y1，x2、y2 是控制点，x3 和 y3 是结束点

就是提供多一个控制点！

画图原理是这样:

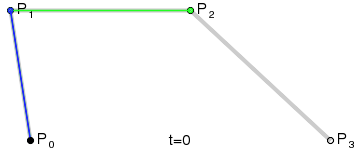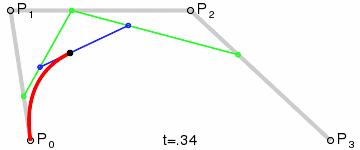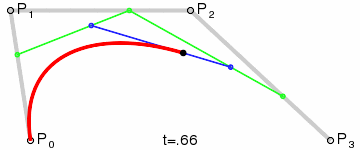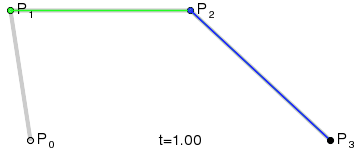
这个例子就不写了，大家照着二次贝塞尔曲线的例子，练习一下！

结束

本次讲了：绘制圆形、绘制弧线、二次贝赛尔曲线、三次贝赛尔曲线，大家学会了多少呢？

好了，本次的教程就到这里结束了，下次将为大家带来线条和文本的操作