python 排序 选择排序

算法思想：

　　首先从序列中选择一个最值，将这个元素和序列的首地址上的元素交换，这样就完成了一个元素的排序，接下来，重复上述过程，不断的从剩下的序列中选取最值，然后添加到有序部分的末尾（注意，这种添加是通过和未排序序列的第一个元素交换来实现的。

　　选择排序每次交换一队元素，他们当中至少有一个元素被移动到了最终位置上，因此对n个元素排序最多需要n-1次排序，这也是选择排序最主要的优点，如果某个元素位于正确的位置上，那么他就不会被移动

　　在所有完全依靠交换去移动元素的排序算法当中，选择排序是非常好的一种

def select_sort2(collection):
    '''选择排序2，通过交换移动位置'''
    #通过交换腾出位置，我竟然没想到，而且这样的好处在于假如一个元素的位置是正确的，在排序的过程中就不用动他
    #所以说，选择排序只需要n-1次交换，他和插入排序的不同再于他总是从未排序的序列中选出来最值，等于说他在未排序中遍历，而插入排序是从未排序
    #的队头取值，在已排序的部分中遍历
    length=len(collection)
    def min_customize(collection):
        min_index=0
        for i in range(len(collection)):
            if collection[i]<collection[min_index]:
                min_index=i
        return min_index
    for loop_index in range(length):
        min_index=min_customize(collection[loop_index:])
        #注意返回的index是部分数组中的
        collection[min_index+loop_index],collection[loop_index]=collection[loop_index],collection[min_index+loop_index]
    return collection

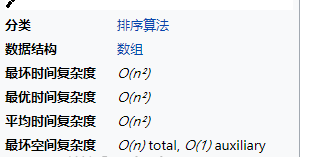
算法分析：

　　空间复杂度：总共需要O(n)（因为要把整个元素放到内存中）额外空间是O(1)，

　　时间复杂度：外层循环执行n次，所以T(n)表达式有n项，而for循环里面还有一个循环，循环里面就是常数操作了，所以每一项都执行这个for循环控制的次数

　　　　需要n次循环，每次循环中需要一次寻找，这个寻找遍历剩余未排序的元素，即与剩下的元素个数有关，.则T(n)=【n+(n-1)+(n-2)+.....+1】（一共n项）=n*(n+1)/2,则T(n)的同数量级是n^2,所以T(n)=O(n^2)

比较

　　与快排比较：随机数据 时间是快排的15倍

详细数据：[0.0319519043, 0.03391861916, 0.03201770782, 0.03198170662, 0.03302311897, 0.03300356865, 0.03403878212, 0.03296375275, 0.03296685219, 0.03298282623, 0.03394627571, 0.03295207024, 0.033979
17747, 0.03199839592, 0.03199625015, 0.03296518326, 0.03206157684, 0.03399348259, 0.03298425674, 0.03299689293, 0.03298187256, 0.03298020363, 0.0319814682, 0.03496980667, 0.03396201134, 0.03299355507, 0.03296756744, 0.03299832344, 0.03498029709, 0.03300309181, 0.03298139572, 0.0329682827, 0.03298211098, 0.03298568726, 0.03297901154, 0.0339858532, 0.03194642067, 0.03199481964, 0.03298521042, 0.03296589851, 0.03397917747, 0.0329811573, 0.03398060799, 0.03194451332, 0.03297448158, 0.03198099136, 0.03399419785, 0.03295683861, 0.03300404549, 0.03198122978, 0.03300428391, 0.03396558762, 0.03598165512, 0.03198719025, 0.03298568726, 0.03193855286, 0.03394913673, 0.03399538994, 0.0329811573, 0.03298187256, 0.03199958801, 0.03397631645, 0.03296804428, 0.03297400475, 0.03197550774, 0.03398966789, 0.03298020363, 0.03299832344, 0.03298711777, 0.03394985199, 0.03297662735, 0.03298425674, 0.03296422958, 0.03396892548, 0.03296399117, 0.03297686577, 0.0329811573, 0.03399586678, 0.03500270844, 0.03398609161, 0.0319814682, 0.03198099136, 0.03195929527, 0.03296470642, 0.03300356865, 0.033005476, 0.03200626373, 0.03298044205, 0.03195428848, 0.03296995163, 0.03296136856, 0.03196334839, 0.03297543526, 0.03398489952, 0.03296351433, 0.03297543526, 0.03298068047, 0.03298139572, 0.03195858002, 0.03398418427]
运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：0.03304997683
前者(选择排序)平均运行时间0.03535942078,后者（快排）平均运行时间0.00230944395,前者约是后者的15.3108倍

　　与插入相比：随即数据，比插入稍慢

详细数据：[0.00201654434, 0.0019993782, 0.00198984146, 0.00099945068, 0.00101208687, 0.0030105114, 0.00300860405, 0.00194263458, 0.0018453598, 0.00098085403, 0.00192856789, 0.00100445747, 0.00198578
835, 0.00199890137, 0.00096893311, 0.00098609924, 0.0019865036, 0.00299334526, 0.0019762516, 0.00197172165, 0.00099682808, 0.00199794769, 0.00403356552, 0.00098729134, 0.00101089478, 0.00097727776, 0.0029630661, 0.00201892853, -0.00098156929, 0.00202488899, 0.0022380352, 0.00198030472, 0.00198173523, 0.00100183487, 0.00099921227, 0.00199460983, 0.00300645828, 0.00099420547, 0.00297141075, 0.00298523903, 0.00198554993, 0.00200295448, 0.00198793411, 0.00198626518, -4.7684e-07, 0.00203299522, 0.00198793411, 0.00198197365, 0.0009996891, 0.00298047066, 0.0009932518, 0.00298452377, -1.335144e-05, 1.239777e-05, 0.00199866295, 0.00199365616, 0.00300693512, 0.00102472305, 0.00199794769, 0.00197958946, 0.0020096302, 0.00200390816, 0.00499773026, 0.00300836563, 0.00100898743, 0.0020031929, 0.00200581551, 0.00099468231, 0.0020031929, 0.00101280212, 0.00199913979, -1.66893e-06, 0.00399661064, 0.00099921227, 0.0019993782, 0.00099921227, 0.00199961662, 0.00198626518, 0.00099849701, -2.622604e-05, 0.00201058388, 1.358986e-05, 0.00297474861, 0.00102519989, 0.00199866295, 0.00100708008, 0.00198221207, 0.00200557709, 0.00301527977, 0.00200414658, 0.00098609924, 0.00200414658, 0.00202178955, 0.00201272964, 0.00198602676, 0.0009996891, -0.0019724369, 0.0010240078, 0.00399971008, 0.0020108223]
运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：0.00175819635
前者(选择排序)平均运行时间0.03519122124,后者（快排）平均运行时间0.03343302488,前者约是后者的1.0526倍

　　与归并相比：比归并慢1个数量级

详细数据：[0.03097867966, 0.03098320961, 0.03198122978, 0.0319814682, 0.03209733963, 0.03298139572, 0.03098201752, 0.03098058701, 0.03298068047, 0.02898454666, 0.03198266029, 0.02898335457, 0.031981
4682, 0.03098201752, 0.02198648453, 0.03098106384, 0.02999019623, 0.03098416328, 0.03101634979, 0.03096461296, 0.03198027611, 0.03298068047, 0.02998232841, 0.03098082542, 0.0309817791, 0.03198170662, 0.03199505806, 0.03098273277, 0.03091812134, 0.03199958801, 0.03196382523, 0.03098058701, 0.03198099136, 0.03198075294, 0.03997635841, 0.03498005867, 0.03098225594, 0.03098225594, 0.02998781204, 0.03098320961, 0.03098225594, 0.03098058701, 0.03198099136, 0.0309817791, 0.03098297119, 0.0319647789, 0.0309650898, 0.03198218346, 0.03198194504, 0.03198170662, 0.03198027611, 0.03098273277, 0.03098225594, 0.03200149536, 0.02998280525, 0.03098249435, 0.03198242188, 0.03198313713, 0.0319814682, 0.03098058701, 0.0319814682, 0.03198242188, 0.03098201752, 0.03098249435, 0.03098297119, 0.0309844017, 0.0309817791, 0.03198266029, 0.03098154068, 0.03198242188, 0.03096580505, 0.03198122978, 0.03099417686, 0.03200078011, 0.03098940849, 0.03297996521, 0.03198242188, 0.03098225594, 0.03098273277, 0.03097867966, 0.03197240829, 0.03098773956, 0.03098225594, 0.02897167206, 0.03196167946, 0.0299885273, 0.03196358681, 0.03000807762, 0.03100061417, 0.03098225594, 0.0309817791, 0.02996611595, 0.03298091888, 0.03096938133, 0.03099489212, 0.03200602531, 0.03195166588, 0.03198099136, 0.03100180626, 0.03198194504]
运行了100次，平均运行时间差(me-other)/(bubble-quick)(正数代表你是个弟弟）是：0.03135284662
前者(选择排序)平均运行时间0.03519077778,后者（快排）平均运行时间0.00383793116,前者约是后者的9.1692倍

　　

　　愚蠢的版本，通过向插入排序那样移动元素来腾出位置（插入排序是不移没有办法，因为，他是在已经有序的部分中找位置，前后都是有序的，而这个不是），要注意思考

def select_sort(collection):
    '''选择排序，通过移动腾出位置'''
    #返回index吧
    #在下面的丢弃过程中其实能寻找出多个最小的值，按照丢弃的顺序就是
    def min_customize(collection):
        min_one_index=0
        for loop_index in range(len(collection)):
            if collection[loop_index]<collection[min_one_index]:
                min_one_index=loop_index
        # print(collection,'中最小的是collection[%d]:%d'%(min_one_index,collection[min_one_index]))
        return min_one_index
    #还要移动，这样移动和上边有重复没有？
    times=0#作为已经有序部分的元素的个数
    while (times<len(collection)):
        min_index=min_customize(collection[times:])+times
        # cache=collection[min_index]#最害怕的就是这个，总是只想一个去的，不想回来的，min_index
        cache=collection[min_index]
        # logging.info('--select_sort()--variable--cache:collection[%d]:%d'%(min_index,collection[min_index]))
        for loop_index in range(min_index,times,-1):#已排序元素个数到这个loop_index
            collection[loop_index]=collection[loop_index-1]
        collection[times]=cache
        times+=1
    return collection