Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable

原文：http://blog.csdn.net/abcjennifer/article/details/7700772

本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。（https://class.coursera.org/ml/class/index）

第二讲-------多变量线性回归 Linear Regression with multiple variable

 

(一)、Multiple Features:

 

多变量假设：输出由多维输入决定，即输入为多维特征。如下图所示：Price为输出，前面四维为输入：

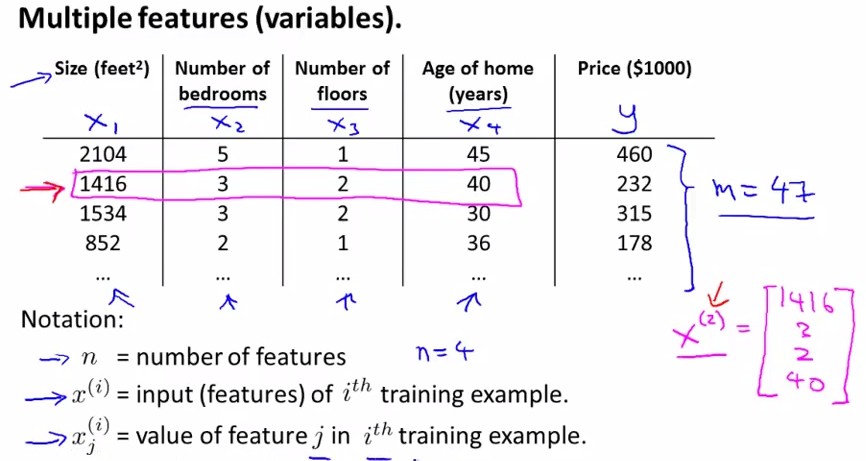
假设h(x)=θ0+θ1x1+……所谓多参数线性回归即每个输入x有(n+1)维[x0……xn]

 

 

 

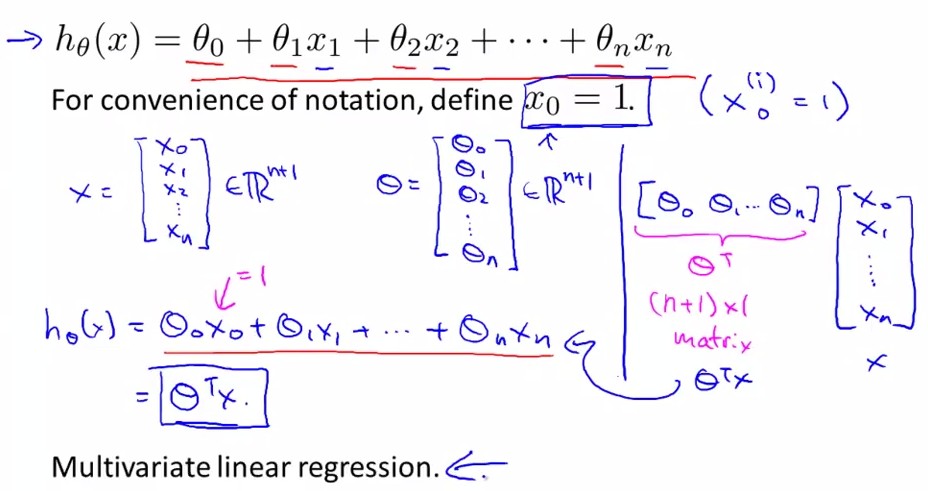
（二）、Gradient Descent for Multiple Variables:

 

左边为但参数的梯度递减单变量学习方法，右图new algorithm为多变量学习方法。

 

 

 

 

 

（三）、Gradient Descent for Multiple Variables - Feature Scaling

 

It is important to 归一化feature，所以用到了feature scaling,即将所有feature归一化到[-1,1]区间内：

归一化方法：xi=(xi-μi)/σi

（四）、Gradient Descent for Multiple Variables - Learning Rate

 

梯度下降算法中另一关键点就是机器学习率的设计：设计准则是保证每一步迭代后都保证能使cost function下降。

这是cost function顺利下降的情况：

这是cost function不顺利下降的情况：

原因如右图所示，由于学习率过大，使得随着迭代次数的增加，J(θ)越跳越大，造成无法收敛的情况。

解决方法：减小学习率

总结：如何选取学习率：

测试α=0.001，收敛太慢（cost function下降太慢），测试0.01，过了？那就0.003……

（五）、Features and Polynomial Regression

 

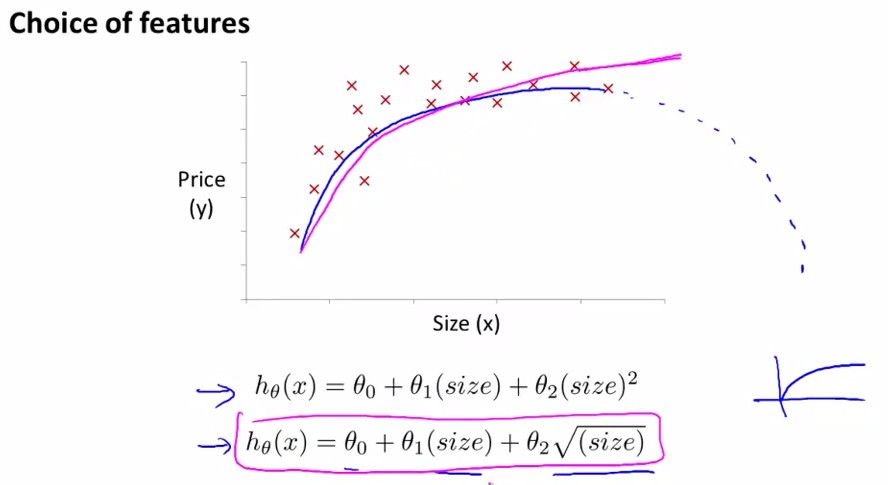
假设我们的输入为一座房子的size，输出为该house的price，对其进行多项式拟合：

有两个选择，二次方程或者三次方程。考虑到二次方程的话总会到最高点后随着size↑，price↓，不合常理；因此选用三次方程进行拟合。

这里归一化是一个关键。

或者有另一种拟合方程，如图粉红色曲线拟合所示：

（六）、Normal Equation

 

与gradient descent平行的一种方法为Normal Equation,它采用线性代数中非迭代的方法，见下图：

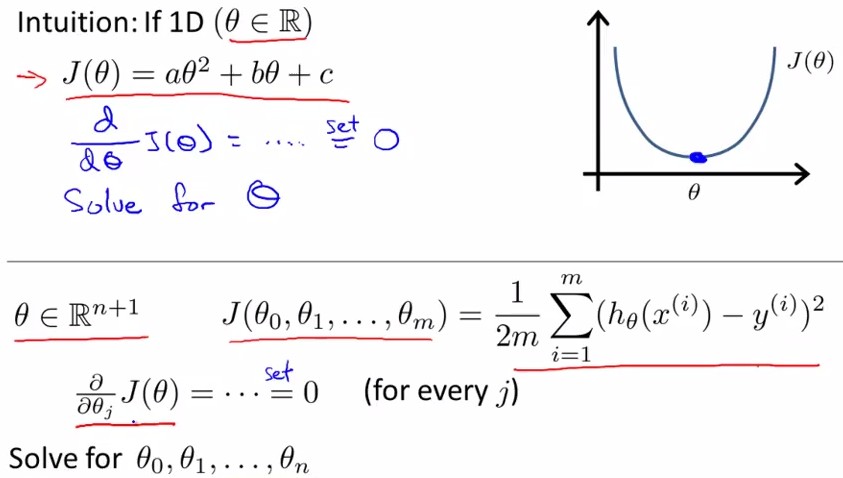
我们想要找到使cost function 最小的θ，就是找到使得导数取0时的参数θ：
该参数可由图中红框公式获得：

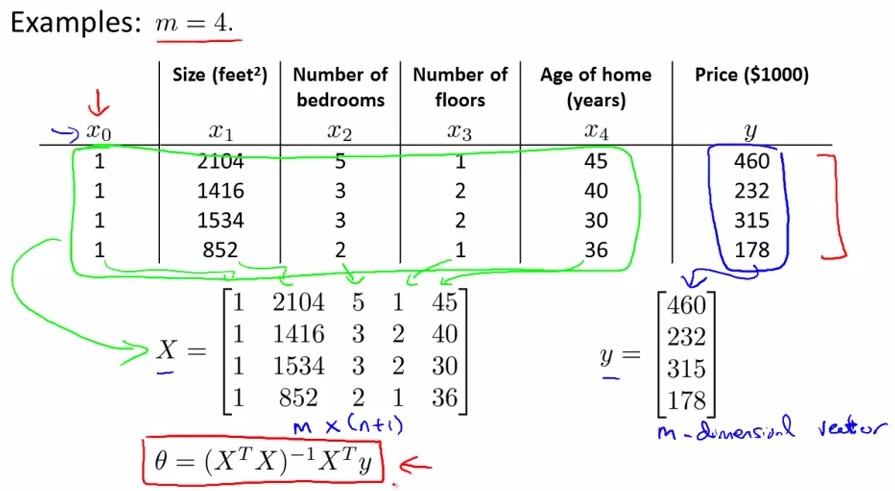
具体来说：X是m×(n+1)的矩阵，y是m×1的矩阵

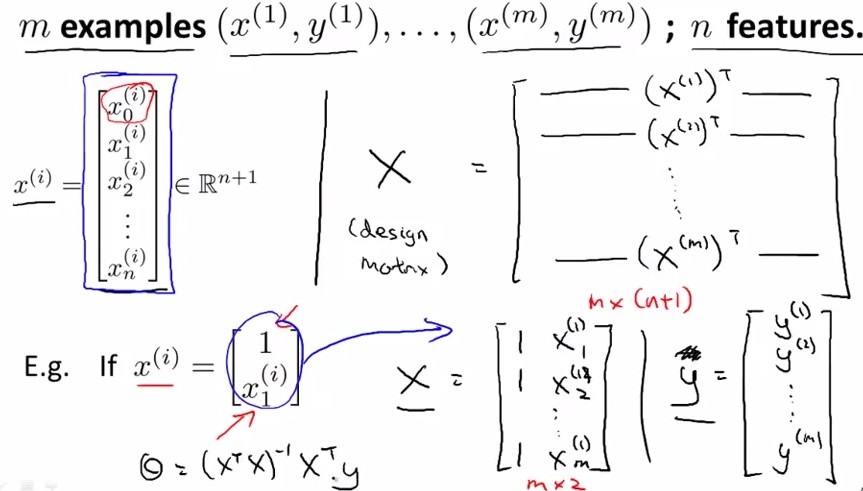
上图中为什么x要加上一列1呢？因为经常设置X⁽ⁱ⁾₀=1；

下面比较一下Gradient Descent与Normal Equation的区别：

（七）、Normal Equation Noninvertibility

 

我们已知，对于有m个样本，每个拥有n个feature的一个训练集，有X是m×(n+1)的矩阵，X^TX是(n+1)×(n+1)的方阵，那么对于参数θ的计算就出现了一个问题，如果|X^TX|=0,即X^TX不可求逆矩阵怎么办？这时可以进行冗余feature的删除（m<=n的情况，feature过多）：