求n*m网格内矩形的数目

一个n*m的网格，求这个网格中矩形的数目。

比如以下2*2网格，总共有9个矩形：4个1*1的矩形，4个1*2的矩形，1个2*2的矩形

 

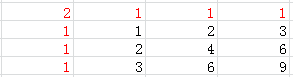
算法1：动态规划，假设dp[i][j]表示以第 i 行第 j 列的格子为右下角顶点的矩形数目，那么dp[i][j] = 1 + dp[i-1][j] + dp[i][j-1] – dp[i-1][j-1] , 这里的1表示i ,j 位置的格子自身构成1*1的矩形，之所以减去dp[i-1][j-1], 因为dp[i-1][j] 和 dp[i][j-1] 都包含了dp[i-1][j-1]。计算时注意i = 1 和 j = 1的边界条件。最后把所有dp[i][j]加起来就是我们所求的答案。以3*3网格举例，为了计算方便，红色为设置的边界值，黑色的才是最后需要加起来的值（结果为36）

 

 

int rectNum(int row, int column)
{
    vector<vector<int> >dp(row+1, vector<int>(column+1, 1));
    int res = 0;
    dp[0][0] = 2;
    for(int i = 1; i <= row; i++)
        for(int j = 1; j <= column; j++)
        {
            dp[i][j] = 1 + dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1];
            res += dp[i][j];
        }
    return res;
}

 

算法2：我们假设网格是1行m列的，那么总的矩形数目 = m(1*1的矩形) + m-1(1*2的矩形) + m-2(1*3的矩形) +…+1(1*m的矩形) = m*(m+1)/2，同理n行1列总的矩形数目是n*(n+1)/2. 对于n*m的网格，我们可以先确定好选取的行数（即确定矩形的高），公共有n*(n+1)/2种选法，选好以后就可以压缩成1行m列的网格来考虑了，因此总共n*(n+1)/2*m*(m+1)/2个矩形。（注意最后结果是否溢出int范围）                 本文地址

int rectNum(int row, int column)
{
    return row*(row+1)*column*(column+1)/4;
}

 

算法2还可以这样理解：两个对角点就可以确定一个矩形。对于一个n*m的网格，总共有（n+1）*（m+1）个顶点，因此第一个顶点有(n+1)*(m+1)种选取方法，选取好第一个顶点后，第二个顶点就有一些限制了，它不能和第一个顶点在同一条直线上，因此第二个顶点有n*m种选取方法；因此选取两个顶点总共有(n+1)*(m+1)*n*m种选取方法，考虑到矩形ABCD，选取AC、CA、BD、DB都表示同一个矩形，即这些选取方法中，包含的每个矩形都重复了四次，因此总共有(n+1)*(m+1)*n*m/4个矩形。

 

可以在hduoj 2524上测试算法的正确性

 

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/3740141.html