k-means 算法介绍

　　　

概述

　　聚类属于机器学习的无监督学习，在数据中发现数据对象之间的关系，将数据进行分组，组内的相似性越大，组间的差别越大，则聚类效果越好。它跟分类的最主要区别就在于有没有“标签”。比如说我们有一组数据，数据对应着每个“标签”，我们通过这些数据与标签之间的相关性，预测出某些数据属于哪些“标签”，这属于分类；而聚类是没有“标签”的，因此说它属于无监督学习，分类则属于监督学习。

　　k-means(k-均值)属于聚类算法之一，笼统点说，它的过程是这样的，先设置参数k，通过欧式距离进行计算，从而将数据集分成k个簇。为了更好地理解这个算法，下面更加详细的介绍这个算法的思想。

算法思想

　　我们先过一下几个基本概念：

　（1） K值：即要将数据分为几个簇；

　（2） 质心：可理解为均值，即向量各个维度取平均值，这个是我们聚类算法一个重要的指标；

　（3） 欧式距离：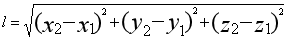

　　上面的这3条基本概念你大可不必太纠结，因为这是为了让你看下面的内容时，能够更好理解。假如说，我们现在有一堆数据集，在图像上的分布是这样的：

　　　　　

　　从图像上看，貌似可以直接把他分为3个簇，因此，我们设置 k=3，然后我们随机生成3个点，再通过欧式距离公式，计算每个点到这三个点之间的距离，距离哪个点最近的，就归类，于是它就变成了这样：

　　　　

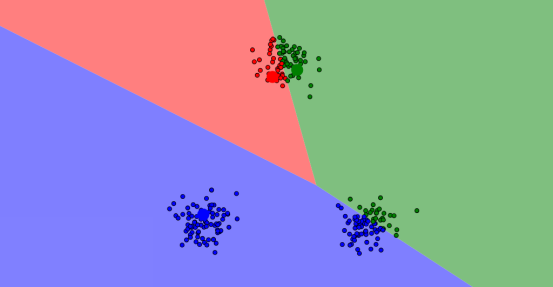
　　当然，这样还不够，毕竟这三个点只是随机生成的，而且我们还需要不断调整以达到更好的聚类效果；因此我们计算初次分好的簇的均值，即上面提到的质心，让这三个质心替代掉随机点，然后迭代重复上面的过程，以达到最优。

　

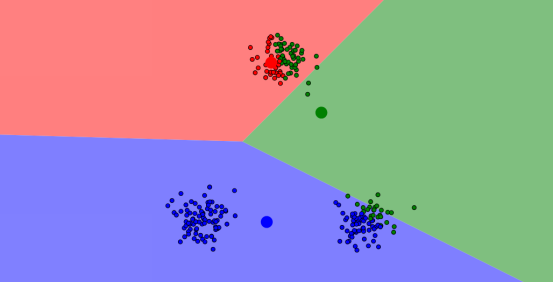
　　......(重复迭代n次)......

　　最后，才生成最优解，如图：

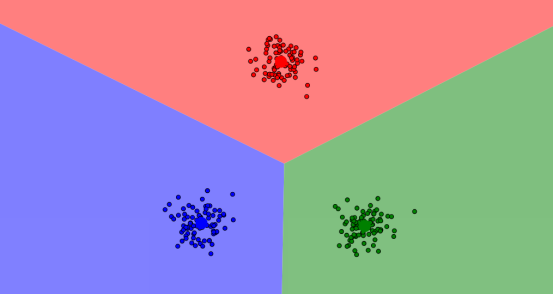
　　上面的图是在这个网站通过演示得到的，可以上这个网址实际操作一波，加深理解。

缺点

　　几乎每个算法都有其缺点，这个算法也不例外，优点是原理简单，实现容易，缺点如下：

　（1）不规则点的聚类结果会有所偏差，如下图，比如我们想分成4个簇，俩眼睛一嘴巴以及外轮廓，但效果总是难以达到。

　　　　　

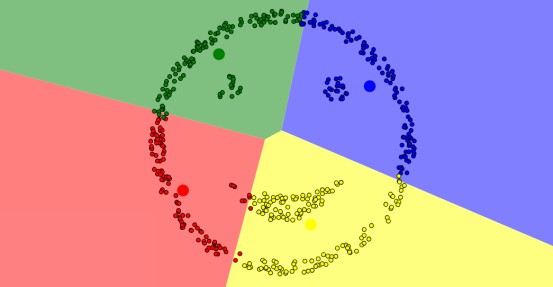
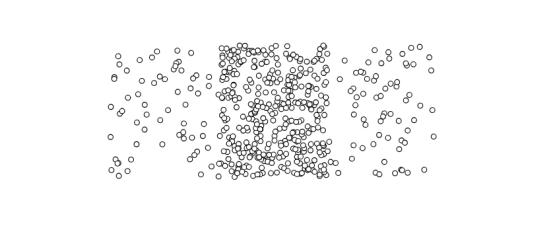
　（2）k值难以确定。比如下面这样的图，应该把它从中间分割得到两块呢还是分成左中右三块呢，难以确定。

　　　　

　　想要第一时间获取更多有意思的推文，可关注公众号： Max的日常操作