Python之机器学习-波斯顿房价预测

目录

• 波士顿房价预测
  • 导入模块
  • 获取数据
    • 打印数据
  • 特征选择
    • 散点图矩阵
    • 关联矩阵
  • 训练模型
  • 可视化

波士顿房价预测

导入模块

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.font_manager import FontProperties
from sklearn.linear_model import LinearRegression
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')

获取数据

  housing-data.txt文件可以加我微信获取：a1171958281

打印数据

df = pd.read_csv('housing-data.txt', sep='\s+', header=0)
df.head()

.dataframe tbody tr th:only-of-type {
vertical-align: middle;
}

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0	0.538	6.575	65.2	4.0900	1	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0	0.469	6.421	78.9	4.9671	2	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0	0.469	7.185	61.1	4.9671	2	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0	0.458	6.998	45.8	6.0622	3	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0	0.458	7.147	54.2	6.0622	3	222.0	18.7	396.90	5.33	36.2

特征选择

散点图矩阵

  使用sns库的pairplot()方法绘制的散点图矩阵可以查看数据集内部特征之间的关系，例如可以观察到特征间分布关系以及离群样本。

  本文只绘制了三列（RM、MEDV(标记)、LSTAT）特征和标记之间的联系，有兴趣的可以调用该方法查看其它特征之间的关系。

# 选择三列特征
cols = ['RM', 'MEDV', 'LSTAT']
# 构造三列特征之间的联系即构造散点图矩阵
sns.pairplot(df[cols], height=3)
plt.tight_layout()
plt.show()

  上图可以看出第一行(RM)第二列(MEDV)的特征与标记存在线性关系；第二行(MEDV)第二列(MEDV)即MEDV值可能呈正态分布。

关联矩阵

  使用sns.heatmap()方法绘制的关联矩阵可以看出特征之间的相关性大小，关联矩阵是包含皮尔森积矩相关系数的正方形矩阵，用来度量特征对之间的线性依赖关系。

# 求解上述三列特征的相关系数
'''
对于一般的矩阵X，执行A=corrcoef(X)后，A中每个值的所在行a和列b，反应的是原矩阵X中相应的第a个列向量和第b个列向量的
相似程度（即相关系数）
'''
cm = np.corrcoef(df[cols].values.T)
# 控制颜色刻度即颜色深浅
sns.set(font_scale=2)
# 构造关联矩阵
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={
                 'size': 20}, yticklabels=cols, xticklabels=cols)
plt.show()

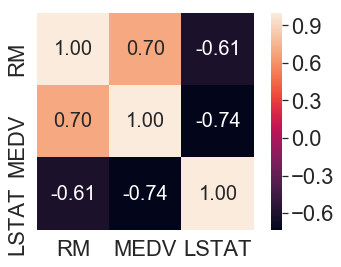
  上图可以看出特征LSTAT和标记MEDV的具有最高的相关性-0.74，但是在散点图矩阵中会发现LSTAT和MEDV之间存在着明显的非线性关系；而特征RM和标记MEDV也具有较高的相关性0.70，并且从散点矩阵中会发现特征RM和标记MEDV之间存在着线性关系。因此接下来将使用RM作为线性回归模型的特征。

训练模型

X = df[['RM']].values
y = df['MEDV'].values

lr = LinearRegression()
lr.fit(X, y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
         normalize=False)

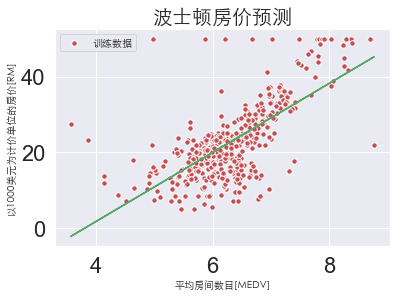
可视化

plt.scatter(X, y, c='r', s=30, edgecolor='white',label='训练数据')
plt.plot(X, lr.predict(X), c='g')
plt.xlabel('平均房间数目[MEDV]', fontproperties=font)
plt.ylabel('以1000美元为计价单位的房价[RM]', fontproperties=font)
plt.title('波士顿房价预测', fontproperties=font, fontsize=20)
plt.legend(prop=font)
plt.show()
print('普通线性回归斜率:{}'.format(lr.coef_[0]))

普通线性回归斜率:9.10210898118031

  使用RANSAC算法之后可以发现线性回归拟合的线与未用RANSAC算法拟合出来的线的斜率不同，可以说RANSAC算法降低了离群值潜在的影响，但是这并不能说明这种方法对未来新数据的预测性能是否有良性影响。