题解报告:hdu 4135 Co-prime(容斥定理入门)
Problem Description
Two integers are said to be co-prime or relatively prime if they have no common positive divisors other than 1 or, equivalently, if their greatest common divisor is 1. The number 1 is relatively prime to every integer.
Input
Output
Sample Input
Sample Output
In the first test case, the five integers in range [1,10] which are relatively prime to 2 are {1,3,5,7,9}.
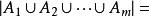
 ,其中选择某几个素因子可以看成是二进制对应bit上的1,如果当前所选个数为奇数,符号为正,否则为负。注意:容斥计数x/p_i中p_i是几个素数的最小公倍数,由于素数之间是互质的,所以可以直接相乘起来作为其最小公倍数。
,其中选择某几个素因子可以看成是二进制对应bit上的1,如果当前所选个数为奇数,符号为正,否则为负。注意:容斥计数x/p_i中p_i是几个素数的最小公倍数,由于素数之间是互质的,所以可以直接相乘起来作为其最小公倍数。#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int t,cnt,prime[];LL a,b,n;
LL solve(LL x){//求与n不互质的总个数
int num;LL ans=,tp;
for(int i=;i<(<<cnt);++i){//用二进制来表示每个质因子是否被使用,即有2^cnt-1种可能,此时cnt较小,题目中1e9最多也就8个素因子,二进制优化
tp=,num=;
for(int j=;j<cnt;++j)
if(i&(<<j))num++,tp*=prime[j];//表示选择哪几个素因子
if(num&)ans+=x/tp;//奇加
else ans-=x/tp;//偶减
}
return x-ans;
}
int main(){
while(~scanf("%d",&t)){
for(int i=;i<=t;++i){
scanf("%lld%lld%lld",&a,&b,&n);cnt=;
for(LL j=;j*j<=n;++j){//求出n内的所有质因子
if(n%j==){
prime[cnt++]=j;
while(n%j==)n/=j;
}
}
if(n>)prime[cnt++]=n;
printf("Case #%d: %lld\n",i,solve(b)-solve(a-));//区间差
}
}
return ;
}
题解报告:hdu 4135 Co-prime(容斥定理入门)的更多相关文章
- HDU 1695 GCD(容斥定理)
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submis ...
- HDU 4135 Co-prime(容斥:二进制解法)题解
题意:给出[a,b]区间内与n互质的个数 思路:如果n比较小,我们可以用欧拉函数解决,但是n有1e9.要求区间内互质,我们可以先求前缀内互质个数,即[1,b]内与n互质,求互质,可以转化为求不互质,也 ...
- HDU 4135 Co-prime(容斥+数论)
Co-prime Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Su ...
- BZOJ2839 : 集合计数 (广义容斥定理)
题目 一个有 \(N\) 个 元素的集合有 \(2^N\) 个不同子集(包含空集), 现在要在这 \(2^N\) 个集合中取出若干集合(至少一个), 使得它们的交集的元素个数为 \(K\) ,求取法的 ...
- HDU 4135 Co-prime 欧拉+容斥定理
Co-prime Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Su ...
- HDU - 4135 Co-prime 容斥定理
题意:给定区间和n,求区间中与n互素的数的个数, . 思路:利用容斥定理求得先求得区间与n互素的数的个数,设表示区间中与n互素的数的个数, 那么区间中与n互素的数的个数等于.详细分析见求指定区间内与n ...
- HDU 1695 GCD 欧拉函数+容斥定理 || 莫比乌斯反演
GCD Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submiss ...
- hdu 6053 trick gcd 容斥
http://acm.hdu.edu.cn/showproblem.php?pid=6053 题意:给定一个数组,我们定义一个新的数组b满足bi<ai 求满足gcd(b1,b2....bn)&g ...
- HDU 2841 Visible Trees(容斥定理)
Visible Trees Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) To ...
随机推荐
- Please verify that your device’s clock is properly set, and that your signing certificate is not exp
真机调试的时候出现此类警告,之前也遇到过,但是一直没总结,今天总结一下 出现这样的问题大概有几个解决方法: 1.最简单的一种----假设你的证书是近期才申请的没什么问题.或者说前几天測试还没问题,突然 ...
- 查询历史使用过的命令并使用(history)
一.什么是history 在bash功能中.它能记忆使用过的命令,这个功能最大的优点就是能够查询以前做过的举动.从而能够知道你的执行步骤.那么就能够追踪你曾下达过的命令.以作为除错的工具. 二.His ...
- hibernate预编译SQL语句中的setParameter和setParameterList
使用预编译SQL语句和占位符參数(在jdbc中是?),可以避免由于使用字符串拼接sql语句带来的复杂性.我们先来简单的看下.使用预编译SQL语句的优点. 使用String sql = "se ...
- armel、armhf和arm64
1 这些名词是什么的缩写 1.1 armel 是arm eabi little endian的缩写.eabi是软浮点二进制接口,这里的e是embeded,是对于嵌入式设备而言. 1.2 armhf 是 ...
- GSON的简单示例
https://github.com/google/gson package com.example.wolf; import com.google.gson.JsonArray; import co ...
- 动态预览Xib的实现
写一个TestView继承于UIView,然后写个对应的xib,把xib的名字设置成TestView,这是标准的用xib加载这个view必须得条件 然后xib里把这个View的backgroundCo ...
- FZU1977 Pandora adventure —— 插头DP
题目链接:https://vjudge.net/problem/FZU-1977 Problem 1977 Pandora adventure Accept: 597 Submit: 2199 ...
- 基于Python 的简单推荐系统
def loadExData(): return[[1,1,1,0,0], [2,2,2,0,0], [1,1,1,0,0], [5,5,5,0,0], [1,1,0,2,2], [0,0,0,3,3 ...
- java的数字精确计算问题-BigDecimal
java的数字运算,偶尔会出现精度的问题,以下阐述的 java的BigDecimal类的使用. 例如: System.out.println(0.9+0.3); 结果1.2 System.out.pr ...
- js 购物车中,多件商品数量加减效果修改,实现总价随数量加减改变
<!DOCTYPE html> <html> <head> <meta charset=UTF-8 /> <title>无标题文档</ ...
