Leetcode 222.完全二叉树的节点个数

完全二叉树的节点个数

给出一个完全二叉树，求出该树的节点个数。

说明：

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^h 个节点。

示例:

输入:

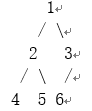
输出: 6

 public class Solution {

     // 获取左子树的高度(其实是最左侧分支）
     public int getLeftHeight(TreeNode root) {
         int count = 0;
         while (root != null) {
             count++;
             root = root.left;
         }
         return count;
     }

     // 获取右子树的高度（其实是最右侧分支的高度）
     public int getRightHeight(TreeNode root) {
         int count = 0;
         while (root != null) {
             count++;
             root = root.right;
         }
         return count;
     }

     public int countNodes(TreeNode root) {
         if (root == null) {
             return 0;
         }
         int leftHeight = getLeftHeight(root);
         int rightHeight = getRightHeight(root);

         if (leftHeight == rightHeight) {
             // 表示是满二叉树，二叉树的节点数直接由公式2^n-1得到
             // leftHeight即为层数， 1 << leftHeight使用位运算计算2^leftHeight，效率更高
             // 注意(1 << leftHeight) - 1 的括号必须有！！
             return (1 << leftHeight) - 1;
         } else {
             // 若该二叉树不是满二叉树，递归的调用该方法，计算左子树和右子树的节点数
             return countNodes(root.left) + countNodes(root.right) + 1;
         }
     }
 }