基于openstack平台的几种Cloud DB解决方案

方案一、openstack 官方 trove解决方案

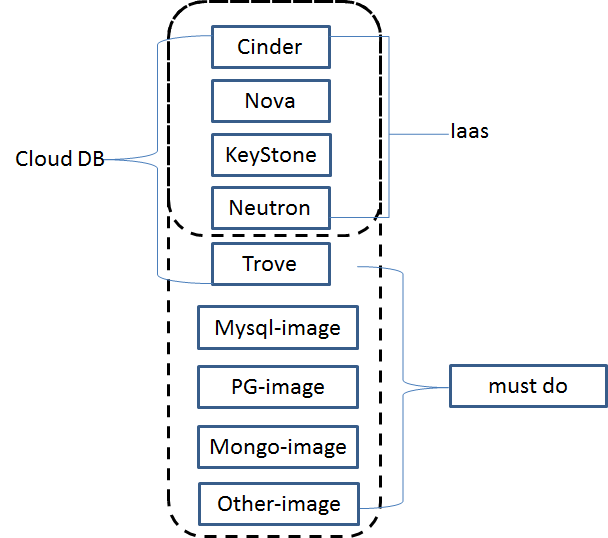
此方案进行过镜像的打包，由于网络问题，还未能成功实现

方案二、salt 或者ansible+ docker

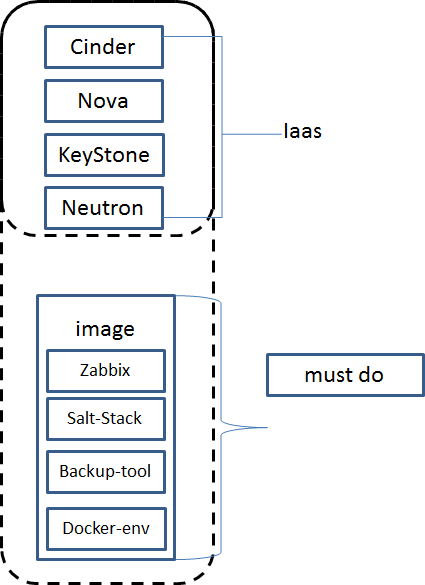
由于 docker部署数据库，在数据库这层上面再加一层docker，数据库性能方面有少许的影响，而且使用docker会打破传统的DB运维，在不考虑运维，性能影响的情况下是可以选择这种Cloud DB部署的

方案三、salt 或者ansible+ db_packagepool+deploy_scripts

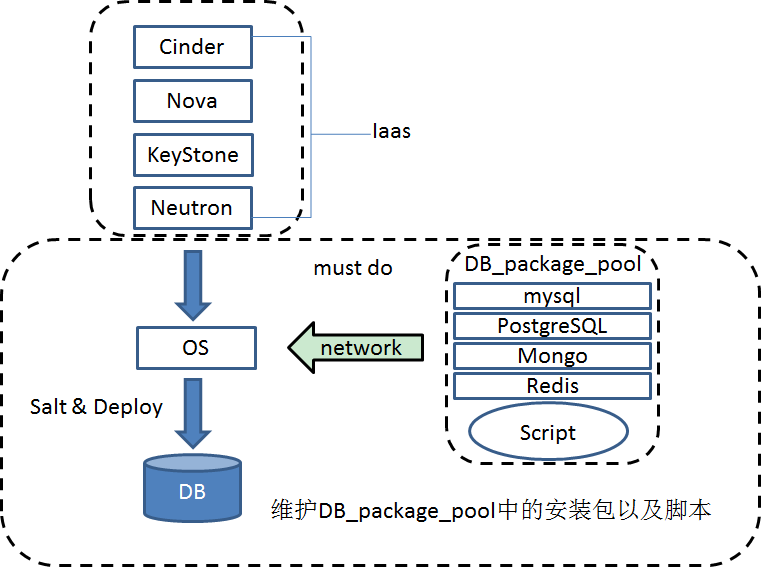
此方案是iaas交付os之后，在此基础上通过网络拉取安装包以及安装脚本，最终交付DB的过程

优点：不需要单独为DB打包镜像包，只需要做各种OS版本的镜像，统一维护db_packagepool的数据库安装包以及安装脚本，维护成本较低

缺点：交付速度缓慢

方案四、salt 或者ansible+DB_package+deploy_scripts

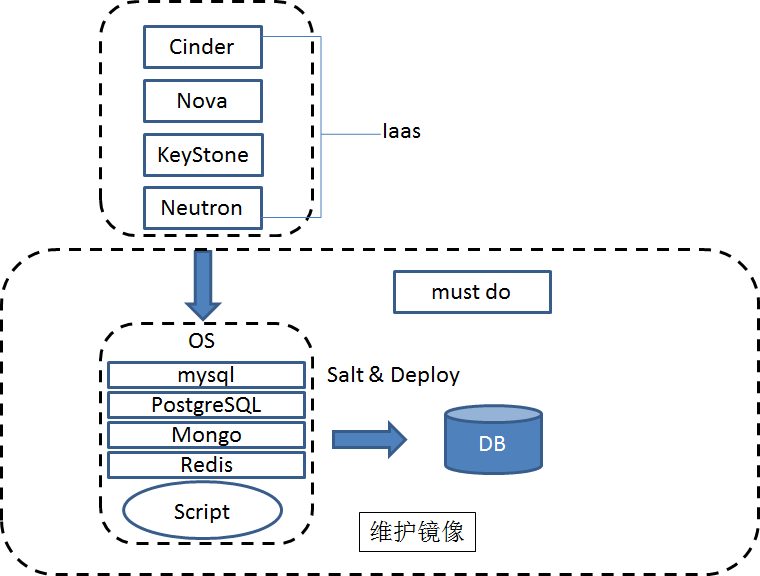
此方案是将数据库安装包以及安装配置脚本都打包到镜像，省去了通过网络拉取安装包的过程，在拉取镜像实例后，可以进行ansible编排或者通过salt agent来进行安装部署

优点：部署过程比方案三快

缺点：维护比较多个版本的镜像文件