最小二乘法拟合非线性函数及其Matlab/Excel 实现（转）

1、最小二乘原理

　　Matlab直接实现最小二乘法的示例：　　

close
x = 1:1:100;
a = -1.5;
b = -10;
y = a*log(x)+b;
yrand = y + 0.5*rand(1,size(y,2));

%%最小二乘拟合
xf=log(x);
yf=yrand;

xfa = [ones(1,size(xf,2));xf]
w = inv(xfa*xfa')*xfa*yf';%直接拟合得到的结果

　　参考资料：

　　1、http://blog.csdn.net/lotus___/article/details/20546259

　　2、http://blog.sina.com.cn/s/blog_5404ea4f0101afth.html

2、matlab调用函数实现最小二乘法

利用matlab的最小二乘拟合函数对非线性函数进行拟合，具体地拟合的函数：

[q r] = lsqcurvefit(fun, q_0, xdata, ydata);
输入参数：
fun：需要拟合的函数，假定有n个需要拟合的参数，那么 q = [q1,q2,...,qn]
q_0：表示用户给定的一个起始点
xdata：函数的自变量
ydata：函数的因变量
输出参数：
q：表示求解得到的最优参数
r：表示最小二乘的目标函数值，即残差。

实现代码

close
x = 1:1:100;
a = -1.5;
b = -10;
y = a*log(x)+b;
plot(x,y);

yrand = y + 0.5*rand(1,size(y,2));
plot(x,yrand,'ro');

%%最小二乘拟合
xf=log(x);
yf=yrand;
f=inline('a(1)+a(2).*x','a','x');
[q,r]=lsqcurvefit(f,[1,0],xf,yf)
plot(x,yrand,'ro','LineWidth',2) %绘制图表
hold on;

%%绘制拟合曲线
yn = q(1)+q(2)*log(x);
hold on;
plot(x,yn,'b','LineWidth',2);

%%设置Legend
hleg = legend(['原始函数(y=' num2str(b,3) '+' num2str(a,3) 'ln(x)' ')数据'],['拟合结果：y=' num2str(q(1),3) '+' num2str(q(2),3) 'ln(x)'],'Location','NorthEast');%本身不能设置字体的大小,需要通过set进行设置
set(hleg,'FontSize', 15, 'FontAngle','italic','FontWeight','bold',...
     'TextColor',[.6,.2,.1],'Color',[1,1,1]);%Color为设置坐标的背景颜色

 %%设置标题
 title('最小二乘拟合：y=a+b*ln(x)','Color','k','FontSize',20);

 %%坐标轴标题设置
 xlabel('x','Color','k','FontSize',15);%横轴标题
 ylabel('y','Color','k','FontSize',15);%纵轴标题

%%保存图像
set(1, 'InvertHardCopy', 'off');%设置的背景色有效,如果为on则图形不保存背景色，maltab 默认为 on
filename = 'lnx';
print(1, '-djpeg', filename);%其他格式 -djpeg,-dpng,-dbmp,-dtiff,-dgif

　　附件：最小二乘matlab.zip

拟合结果

如下图所示

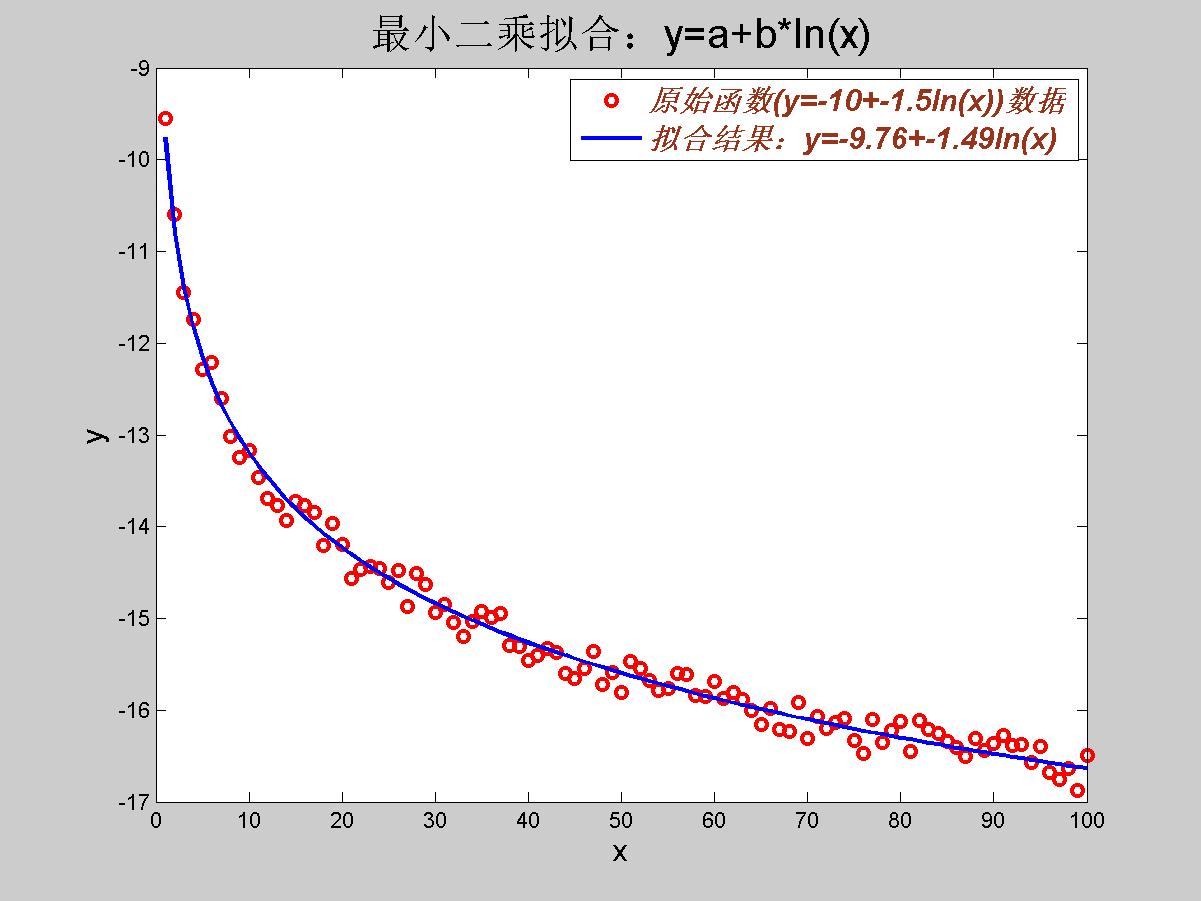
3、Excel的实现

使用 lenest函数进行最小二乘拟合，对以上生成的数据进行拟合，拟合结果和matlab是一致的。

已知拟合函数y=ax+b,那么

斜率计算公式为：

　　a = lenest(ydata,xdata,,FALSE)

截距计算公式为：

　　b = index(lenest(ydata,xdata),,FALSE),2)

拟合的代码，请查阅附件：最小二乘拟合.xlsx，包含了带噪声的原始数据，拟合公式，拟合结果图

拟合结果如下图所示：

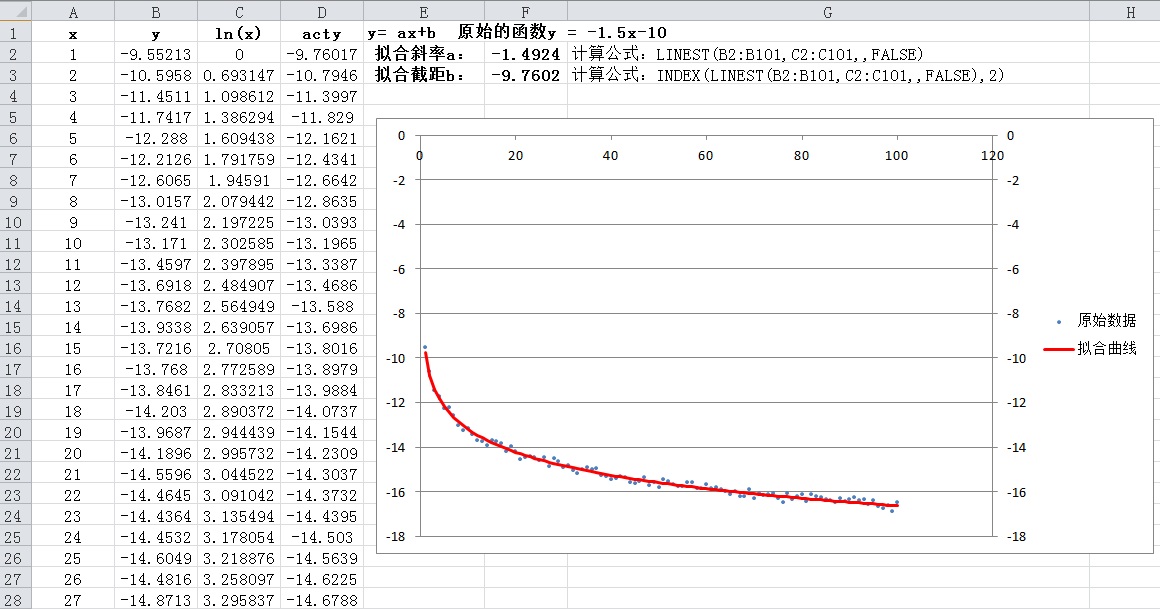
http://www.cnblogs.com/cv-pr/p/4741262.html