hdu 4444 Walk （离散化+建图+bfs+三维判重 好题）

Walk

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 1142    Accepted Submission(s): 195

Problem Description

Biaoge is planning to walk to amusement park. The city he lives can be abstracted as a 2D plane. Biaoge is at (x1, y1) and the amusement park is at (x2, y2). There are also some rectangle buildings. Biaoge can only walk parallel to the coordinate axis. Of course Biaoge can’t walk across the buildings.

What’s the minimum number of turns Biaoge need to make?

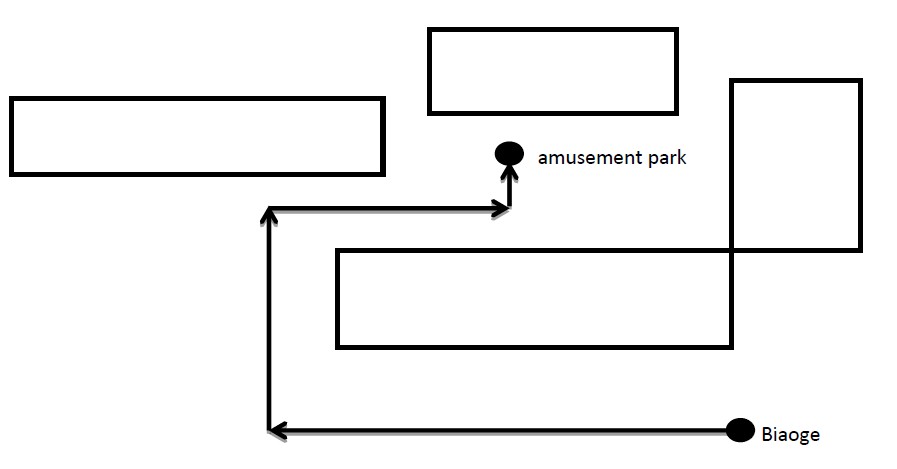
As the figure above shows, there are 4 buildings and Biaoge need to make at least 3 turns to reach the amusement park(Before walking he can chose a direction freely). It is guaranteed that all the buildings are parallel to the coordination axis. Buildings may contact but overlapping is impossible. The amusement park and Biaoge’s initial positions will not contact or inside any building.

 

Input

There are multiple test case.

Each test case contains several lines.

The first line contains 4 integers x1, y1, x2, y2 indicating the coordinate of Biaoge and amusement park.

The second line contains one integer N(0≤N≤50), indicating the number of buildings.

Then N lines follows, each contains 4 integer x1, y1, x2, y2, indicating the coordinates of two opposite vertices of the building.

Input ends with 0 0 0 0, you should not process it.

All numbers in the input range from -10
⁸ to 10
⁸.

 

Output

For each test case, output the number of least turns in a single line. If Biaoge can’t reach the amusement park, output -1 instead.

 

Sample Input

0 0 0 10
1
0 5 5 8
0 0 0 10
2
0 5 5 8
-2 1 0 5
0 0 0 0

 

Sample Output

0
2

Hint

In the first case, Biaoge can walk along the side of building, and no turn needed.
In the second case, two buildings block the direct way and Biaoge need to make 2 turns at least.

 

Source

2012 Asia JinHua Regional Contest

感想：

哇哈哈，这题搞了一天终于搞出来啦！  早上开始研究一个人的代码（很简洁，风格很好），研究了一个早上，思想都懂了，然后下午开始自己写，写出来后测别人贴的数据，发现最后一组数据怎么也过不了，又仔细研究了一会，发现这种思路就是错的。 我 X_X ，当时就有砸电脑的冲动了，白白浪费我我这么长时间。   ps：这题区域赛时数据水了，所以有些代码页就水过了，所以提供的解题报告有些就是错的。然后下午又重新开始搞，看了一个人的思路觉得很正确，然后晚上就开始按照这种思路写，写出来了也是各种debug，各种改代码，最后终于AC了，那叫一个爽呀！

题意：

二维平面内给n个矩形，再给2个点，求两点之间所有路径中最少的拐弯次数。

思路：

离散化矩形，因为矩形边界可以走，所以还是有点麻烦的，将一个1*1的方格看做3*3的方格后就好处理了。最重要的问题就是该怎样表示矩形。

我是这样做的：将矩形覆盖区域涂黑（标记为1），注意不能全部涂黑，不然边界也不能走了，每次将矩形涂黑时，要将矩形左边界＋1，右边界－1，上下界也同样。这样矩形的边界就可以走了。但是这又会出现另一种情况，就是有两个相邻的矩形时，它们的边界是不能走的。我们可以这样判断一个点能否往上走：如果它所在的3*3的方格的上方的点左边和右边都是黑的，那么它就不能往上走。（下、左、右同理） 最纠结的就是拐点处了（“L”型区域） 这个就必须特判了，有8种情况，自己把情况想清楚了再写。

图建好了之后就和“hdu 1728” 一样了，就不多说了。

注意：

1.边界情况很重要 横边界能横着走，不能竖着走，竖边界同理。

2.‘L’型区域要特殊处理，有8种情况，要好好分析。

3.一个点可能走多次，不能简单的二维判重，要加上方向。（比如我贴的最后一组数据）

ps：思路来源于：http://blog.csdn.net/asdfgh0308/article/details/8125832

        数据来源于：http://blog.csdn.net/ophunter/article/details/9768855#comments

自己方便debug，加了几个show函数，加了几个中间输出，代码变长了一点。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 350
using namespace std;

int n,m,ans;
int sx,sy,ex,ey;
int x[maxn],y[maxn];
int xx[maxn],yy[maxn];
int mp[maxn][maxn];
int up[maxn][maxn],down[maxn][maxn];
int le[maxn][maxn],ri[maxn][maxn];
int dx[]= {-3,3,0,0};
int dy[]= {0,0,-3,3};
bool vis[maxn][maxn][4];  // 三维判重 x+y+方向
struct Node
{
    int l,d,r,u;
} rect[maxn];
struct node
{
    int mx,my;
    int d,cnt;   // 方向 转向次数
} cur,now,q[maxn*maxn];

void showxxyy()  // 输出离散化后的x y
{
    int i,j;
    printf("xx:\n");
    for(i=1; i<=m; i++)
    {
        printf("%d ",xx[i]);
    }
    printf("\n");
    printf("yy:\n");
    for(i=1; i<=m; i++)
    {
        printf("%d ",yy[i]);
    }
    printf("\n");
}
void showmap()  // 输出地图
{
    int i,j;
    printf("showmap:\n");
    printf("       1  2  3  4  5  6  7  8  9  10 11 12 \n");
    for(i=1; i<=3*xx[m]; i++)
    {
        printf("%3d: ",i);
        for(j=1; j<=3*yy[m]; j++)
        {
            printf("%d",mp[i][j]);
        }
        printf("\n");
    }
}
void disc()   // 离散化
{
    int i,j;
    m=2*n+2;
    sort(x+1,x+m+1);
    xx[1]=1;
    for(i=2; i<=m; i++)
    {
        if(x[i]==x[i-1]) xx[i]=xx[i-1];
        else xx[i]=xx[i-1]+1;
    }
    sort(y+1,y+m+1);
    yy[1]=1;
    for(i=2; i<=m; i++)
    {
        if(y[i]==y[i-1]) yy[i]=yy[i-1];
        else yy[i]=yy[i-1]+1;
    }
//    showxxyy();
}
int find(int v,int k)   // 找到离散化对应的点
{
    int i,j;
    if(k)
    {
        for(i=1; i<=m; i++)
        {
            if(y[i]==v) return yy[i];
        }
    }
    else
    {
        for(i=1; i<=m; i++)
        {
            if(x[i]==v) return xx[i];
        }
    }
}
void buildgraph()  // 将1*1的方格转化为3*3的方格后建图
{
    int i,j,ni,nj,k,l,d,r,u;
    memset(mp,0,sizeof(mp));
    memset(up,1,sizeof(up));
    memset(down,1,sizeof(down));
    memset(le,1,sizeof(le));
    memset(ri,1,sizeof(ri));
    for(k=1; k<=n; k++)  // 将矩形在地图上涂黑
    {
        l=3*find(rect[k].l,0)+1;
        d=3*find(rect[k].d,1)+1;
        r=3*find(rect[k].r,0)-1;
        u=3*find(rect[k].u,1)-1;
//        printf("l:%d d:%d r:%d u:%d\n",l,d,r,u);
        for(i=l; i<=r; i++)
        {
            for(j=d; j<=u; j++)
            {
                mp[i][j]=1;
            }
        }
    }
    for(i=1; i<=xx[m]; i++)  // 记录是否能走 是否是‘L’型区域
    {
        for(j=1; j<=yy[m]; j++)
        {
            ni=3*i;
            nj=3*j;
            if(mp[ni-1][nj-1]&&mp[ni+1][nj+1])
            {
                up[ni][nj]=down[ni][nj]=le[ni][nj]=ri[ni][nj]=-1;
            }
            else if(mp[ni+1][nj-1]&&mp[ni-1][nj+1]) up[ni][nj]=down[ni][nj]=le[ni][nj]=ri[ni][nj]=-2;
            if(mp[ni-1][nj-1]&&mp[ni-1][nj+1]) up[ni][nj]=0;
            if(mp[ni+1][nj-1]&&mp[ni+1][nj+1]) down[ni][nj]=0;
            if(mp[ni-1][nj-1]&&mp[ni+1][nj-1]) le[ni][nj]=0;
            if(mp[ni-1][nj+1]&&mp[ni+1][nj+1]) ri[ni][nj]=0;
        }
    }
//    showmap();
}
bool bfs() // 图建好了 就是简单的bfs了
{
    int i,j,nx,ny,nd,ncnt,tx,ty;
    int head=0,tail=-1;
    memset(vis,0,sizeof(vis));
    sx=3*find(sx,0);
    sy=3*find(sy,1);
    ex=3*find(ex,0);
    ey=3*find(ey,1);
//    printf("sx:%d sy:%d ex:%d ey:%d\n",sx/3,sy/3,ex/3,ey/3);
    cur.mx=sx;
    cur.my=sy;
    cur.d=-1;
    cur.cnt=0;
    vis[sx][sy][0]=vis[sx][sy][1]=vis[sx][sy][2]=vis[sx][sy][3]=1;
    q[++tail]=cur;
    while(head<=tail)
    {
        now=q[head];
        head++;
        nx=now.mx;
        ny=now.my;
        nd=now.d;
        ncnt=now.cnt;
//        printf("nx:%d ny:%d nd:%d ncnt:%d\n",nx/3,ny/3,nd,ncnt);
        if(nx==ex&&ny==ey)
        {
            ans=ncnt;
            return true ;
        }
        for(i=0; i<4; i++)
        {
            if(i==0&&!up[nx][ny]||i==1&&!down[nx][ny]||i==2&&!le[nx][ny]||i==3&&!ri[nx][ny]) continue ; // 判断是否能往这个方向走
            if(up[nx][ny]==-1)    // 对‘L’型区域特判
            {
                if(i==0&&(nd==0||nd==3)) continue ;
                else if(i==1&&(nd==1||nd==2)) continue ;
                else if(i==2&&(nd==2||nd==1)) continue ;
                else if(i==3&&(nd==3||nd==0)) continue ;
            }
            else if(up[nx][ny]==-2)
            {
                if(i==0&&(nd==0||nd==2)) continue ;
                else if(i==1&&(nd==1||nd==3)) continue ;
                else if(i==2&&(nd==2||nd==0)) continue ;
                else if(i==3&&(nd==3||nd==1)) continue ;
            }
            tx=nx+dx[i];
            ty=ny+dy[i];
            while(tx>=1&&tx<=3*xx[m]&&ty>=1&&ty<=3*yy[m]&&!mp[tx][ty]) // 每次向一个方向搜索
            {
                if(!vis[tx][ty][i])
                {
                    vis[tx][ty][i]=1;
                    cur.mx=tx;
                    cur.my=ty;
                    cur.d=i;
                    cur.cnt=ncnt;
                    if(cur.d!=nd&&nd!=-1) cur.cnt++;
                    q[++tail]=cur;
                }
                if(i==0&&!up[tx][ty]||i==1&&!down[tx][ty]||i==2&&!le[tx][ty]||i==3&&!ri[tx][ty]) break ;
                if(up[tx][ty]==-1||up[tx][ty]==-2) break ;
                tx+=dx[i];
                ty+=dy[i];
            }
        }
    }
    return false ;
}
int main()
{
    int i,j;
    int x1,y1,x2,y2,l,d,r,u;
    while(scanf("%d%d%d%d",&sx,&sy,&ex,&ey),sx||sy||ex||ey)
    {
        scanf("%d",&n);
        for(i=1; i<=n; i++)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            l=min(x1,x2);
            r=max(x1,x2);
            d=min(y1,y2);
            u=max(y1,y2);
            x[i]=rect[i].l=l;
            x[i+n]=rect[i].r=r;
            y[i]=rect[i].d=d;
            y[i+n]=rect[i].u=u;
        }
        x[2*n+1]=sx;
        x[2*n+2]=ex;
        y[2*n+1]=sy;
        y[2*n+2]=ey;
        disc();
        buildgraph();
        if(bfs()) printf("%d\n",ans);
        else printf("-1\n");
    }
    return 0;
}
/*

// 绕路   2
1 1 1 4
1
0 2 2 3

// 直走  0
1 1 1 4
1
3 3 4 5

// 沿着边直走  0
0 1 0 7
2
0 2 2 3
-1 4 0 5

// 沿着边直走  0
0 1 0 7
2
0 2 2 3
0 3 2 4

// 无法穿过缝隙，绕路   2
0 1 0 7
2
0 2 2 3
-1 3 0 5

// 无法到达  -1
0 0 5 5
4
-1 1 1 2
1 -1 2 1
-1 -1 1 -2
-1 1 -2 -1

// 同点经过两次。  5
1 3 4 1
10
-1 -1 3 2
3 -1 7 0
7 -1 11 3
9 3 11 7
-1 7 11 9
0 5 4 7
-1 2 0 7
2 2 4 3
4 3 5 4
5 4 8 6
*/