决策树ID3算法

决策树 (Decision Tree）是在已知各种情况发生概率的基础上，通过构成 决策树 来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称 决策树 。在机器学习中，决策树 是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系。Entropy = 系统的凌乱程度，使用算法ID3, C4.5和C5.0生成树算法使用熵。这一度量是基于信息学理论中熵的概念，本文着重讲ID3算法。

假设存在如下一组信息：

天气	气温	湿度	风	外出
晴朗	高温	高	无风	no
晴朗	高温	高	有风	no
多云	高温	高	无风	yes
下雨	温暖	高	无风	yes
下雨	寒冷	正常	无风	yes
下雨	寒冷	正常	有风	no
多云	寒冷	正常	有风	yes
晴朗	温暖	高	无风	no
晴朗	寒冷	正常	无风	yes
下雨	温暖	正常	无风	yes
晴朗	温暖	正常	有风	yes
多云	温暖	高	有风	yes
多云	高温	正常	无风	yes
下雨	温暖	高	有风	no

假如时间发生发概率为(p1,p2,...,pn)，那么可以定义信息熵为：

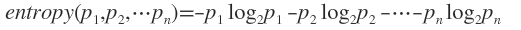
例如外出的概率是9/14，不外出的概率是5/14，那么 外出的信息熵entropy 为：

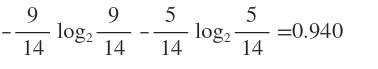
将上面的表格整理一下如下：

天气	yes	no	气温	yes	no	湿度	yes	no	风	yes	no	外出	yes	no
晴朗	2	3	高温	2	2	高	3	4	无风	6	2	外出	9	5
多云	4	0	温暖	4	2	正常	6	1	有风	3	3
下雨	3	2	寒冷	3	1

各个天气情况 的信息熵计算为：

• 天气为晴朗时，2/5的概率外出，3/5的概率不外出，信息熵为0.971

• 天气为多云时，信息熵为0

• 天气为下雨时，3/5的概率外出，2/5的概率不外出，信息熵为0.971

而天气是 晴朗 的概率为5/14，天气是 多云 的概率为4/14，天气是 下雨 的概率为5/14，所以 天气 的信息熵为：

5/14 × 0.971 + 4/14 × 0 + 5/14 × 0.971 = 0.693

天气的 信息增益gain 为：

0.940-0.693=0.247

同理 温度gain 为0.029， 湿度gain 为0.152，风gain 为0.048

天气的信息熵下降得最快，所以决策树的根节点为 天气 ，子节点为 晴朗 、多云 、下雨 ：

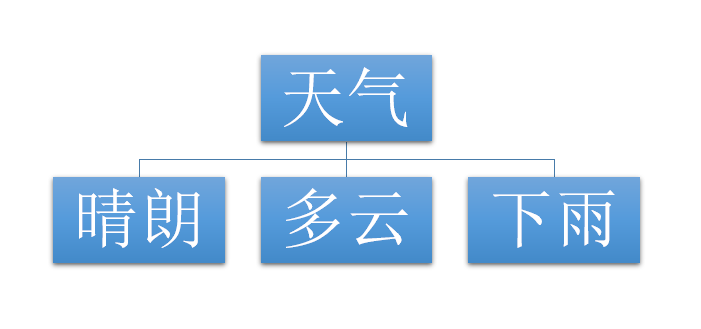
根据第一个表格得知，天气 晴朗 的日子有5天，这5天对应各种不一样的 气温 、 湿度 、 风 、 外出 ，如下：

晴朗 {'湿度': ['高', '高', '高', '正常', '正常'], '风': ['无风', '有风', '无风', '无风', '有风'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}
下雨 {'湿度': ['高', '正常', '正常', '正常', '高'], '风': ['无风', '无风', '有风', '无风', '有风'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
多云 {'湿度': ['高', '正常', '高', '正常'], '风': ['无风', '有风', '有风', '无风'], '气温': ['高温', '寒冷', '温暖', '高温']}

多云 ['yes', 'yes', 'yes', 'yes']
晴朗 ['no', 'no', 'no', 'yes', 'yes']
下雨 ['yes', 'yes', 'no', 'yes', 'no']

在前面计算，由于 多云 的信息熵为0，所以多云的时候是一定会外出的，即 多云=yes ：

晴朗 {'湿度': ['高', '高', '高', '正常', '正常'], '风': ['无风', '有风', '无风', '无风', '有风'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}
下雨 {'湿度': ['高', '正常', '正常', '正常', '高'], '风': ['无风', '无风', '有风', '无风', '有风'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
多云 'yes'

多云 'yes'
晴朗 ['no', 'no', 'no', 'yes', 'yes']
下雨 ['yes', 'yes', 'no', 'yes', 'no']

此时需要再次计算：

1. 晴朗条件下，湿度、风、气温那个的信息增益下降最快，选取下降最快的为晴朗的下一个节点
2. 下雨条件下，湿度、风、气温那个的信息增益下降最快，选取下降最快的为下雨的下一个节点
3. 再次判断哪一个信息熵变成了0，变成了0则可以终止这一条树

经过代码计算， 晴朗 的下一个节点为 湿度 ， 下雨 的下一个节点为 风 ，以此继续递归下去.

---

python代码为

整理的原始数据为：

condition = {'风': ['无风', '有风', '无风', '无风', '无风', '有风', '有风', '无风', '无风', '无风', '有风', '有风', '无风', '有风'],
                 '湿度': ['高', '高', '高', '高', '正常', '正常', '正常', '高', '正常', '正常', '正常', '高', '正常', '高'],
                 '天气': ['晴朗', '晴朗', '多云', '下雨', '下雨', '下雨', '多云', '晴朗', '晴朗', '下雨', '晴朗', '多云', '多云', '下雨'],
                 '气温': ['高温', '高温', '高温', '温暖', '寒冷', '寒冷', '寒冷', '温暖', '寒冷', '温暖', '温暖', '温暖', '高温', '温暖']}
result = {'外出': ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']}

计算各种情况出现的概率：

# 计算出现的概率
def CalcProbability(array):
    dict = {}
    count = Counter(array)
    for item in count:
        dict[item] = count[item] / len(array)
    return dict

计算信息熵：

# 计算信息熵
def CalcEntropy(array):
    entropy = 0
    for i in range(0, len(array)):
        entropy = entropy + (-array[i] * math.log2(array[i]))
    return entropy

将原数据变为这样的样式：

天气	yes	no	气温	yes	no	湿度	yes	no	风	yes	no	外出	yes	no
晴朗	2	3	高温	2	2	高	3	4	无风	6	2	外出	9	5
多云	4	0	温暖	4	2	正常	6	1	有风	3	3
下雨	3	2	寒冷	3	1

# 重新整理数据
def Statistics(condition, result):
    # 获得各种结果出现的概率
    for k in result:
        resultProbability = CalcProbability(result[k])
    # {'no': 0.35714285714285715, 'yes': 0.6428571428571429}
    # 获得结果的信息熵
    resultarr = []
    for key in resultProbability:
        resultarr.append(resultProbability[key])
    resultEntropy = CalcEntropy(resultarr)
    # print(resultEntropy)
    # 0.9402859586706311

    # 统计各个条件下的外出结果
    dict = {}
    for key in condition.keys():
        tempdict = {}
        for i in range(0, len(condition[key])):
            if condition[key][i] in tempdict:
                for k in result:
                    tempdict[condition[key][i]].append(result[k][i])
            else:
                arr = []
                for k in result:
                    arr.append(result[k][i])
                tempdict[condition[key][i]] = arr
        dict[key] = tempdict
        # print(dict)
        # {'风': {'有风': ['no', 'no', 'yes', 'yes', 'yes', 'no'], '无风': ['no', 'yes', 'yes', 'yes', 'no', 'yes', 'yes', 'yes']}, '湿度': {'正常': ['yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes'], '高': ['no', 'no', 'yes', 'yes', 'no', 'yes', 'no']}, '天气': {'晴朗': ['no', 'no', 'no', 'yes', 'yes'], '下雨': ['yes', 'yes', 'no', 'yes', 'no'], '多云': ['yes', 'yes', 'yes', 'yes']}, '气温': {'温暖': ['yes', 'no', 'yes', 'yes', 'yes', 'no'], '寒冷': ['yes', 'no', 'yes', 'yes'], '高温': ['no', 'no', 'yes', 'yes']}}
    # 计算不同外出情况下的信息熵
    newdict = {}
    for keys in dict:
        tempdict = {}
        for key in dict[keys]:
            temp = CalcProbability(dict[keys][key])
            temparr = []
            for value in temp:
                temparr.append(temp[value])
                tempdict[key] = CalcEntropy(temparr)
            newdict[keys] = tempdict
    # print(newdict)
    # {'风': {'无风': 0.8112781244591328, '有风': 1.0}, '天气': {'多云': 0.0, '晴朗': 0.9709505944546686, '下雨': 0.9709505944546686}, '湿度': {'高': 0.9852281360342516, '正常': 0.5916727785823275}, '气温': {'温暖': 0.9182958340544896, '寒冷': 0.8112781244591328, '高温': 1.0}}

    # 不同条件出现的概率
    conditiondict = {}
    for item in condition:
        conditiondict[item] = CalcProbability(condition[item])
    # print(conditiondict)
    # {'气温': {'高温': 0.2857142857142857, '温暖': 0.42857142857142855, '寒冷': 0.2857142857142857}, '风': {'有风': 0.42857142857142855, '无风': 0.5714285714285714}, '湿度': {'高': 0.5, '正常': 0.5}, '天气': {'晴朗': 0.35714285714285715, '下雨': 0.35714285714285715, '多云': 0.2857142857142857}}

    return resultEntropy, newdict, conditiondict

计算信息增益：

# 计算信息增益
def CalcGain(resultEntropy, conditionEntropy, conditionProbability):
    conditionGain = {}
    for keys in conditionEntropy:
        number = 0
        for key in conditionEntropy[keys]:
            number = number + conditionEntropy[keys][key] * conditionProbability[keys][key]
        conditionGain[keys] = resultEntropy - number
    # reverse=True值按照从大到小排序
    conditionGain = sorted(conditionGain.items(), key=lambda d: d[1], reverse=True)

    return conditionGain

最终递归：

# 递归计算咯
def recursion(condition, result):
    resultEntropy, conditionEntropy, conditionProbability = Statistics(condition, result)
    # print(resultEntropy)
    # print(conditionEntropy)
    # print(conditionProbability)
    conditionGain = CalcGain(resultEntropy, conditionEntropy, conditionProbability)
    # print(conditionGain)

    # 哦按段是否为零
    key = conditionGain[0][0]
    value = ""
    for values in conditionEntropy[key]:
        if conditionEntropy[key][values] == 0:
            value = values

    kinds = []
    for item in condition[key]:
        if item in kinds:
            pass
        else:
            kinds.append(item)
    # ['晴朗', '多云', '下雨']

    # 删除天气这个key
    arrcondition = condition[key]
    condition.pop(key)
    # print("sssssssss",key)
    newcondition = {}
    newresult = {}
    for item in kinds:
        dict = {}
        resultarr = []
        for i in range(0, len(arrcondition)):
            if arrcondition[i] == item:
                for keys in condition:
                    if keys in dict:
                        dict[keys].append(condition[keys][i])
                    else:
                        temparr = []
                        temparr.append(condition[keys][i])
                        dict[keys] = temparr
                for key in result:
                    resultarr.append(result[key][i])
                    newresult[item] = resultarr
            newcondition[item] = dict

    # print(newcondition)
    # {'多云': {'气温': ['高温', '寒冷', '温暖', '高温'], '风': ['无风', '有风', '有风', '无风'], '湿度': ['高', '正常', '高', '正常']}, '晴朗': {'气温': ['高温', '高温', '温暖', '寒冷', '温暖'], '风': ['无风', '有风', '无风', '无风', '有风'], '湿度': ['高', '高', '高', '正常', '正常']}, '下雨': {'气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖'], '风': ['无风', '无风', '有风', '无风', '有风'], '湿度': ['高', '正常', '正常', '正常', '高']}}
    # print(newresult)
    # {'多云': ['yes', 'yes', 'yes', 'yes'], '晴朗': ['no', 'no', 'no', 'yes', 'yes'], '下雨': ['yes', 'yes', 'no', 'yes', 'no']}

    if value in newcondition:
        newcondition[value] = "yes"
    # 得到的新condition为dict：
    # '多云': 'yes'
    # 下雨 {'风': ['无风', '无风', '有风', '无风', '有风'], '湿度': ['高', '正常', '正常', '正常', '高'], '气温': ['温暖', '寒冷', '寒冷', '温暖', '温暖']}
    # 晴朗 {'风': ['无风', '有风', '无风', '无风', '有风'], '湿度': ['高', '高', '高', '正常', '正常'], '气温': ['高温', '高温', '温暖', '寒冷', '温暖']}

    # 得到的新result为newresult：
    # 多云 ['yes', 'yes', 'yes', 'yes']
    # 晴朗 ['no', 'no', 'no', 'yes', 'yes']
    # 下雨 ['yes', 'yes', 'no', 'yes', 'no']

    print(newcondition)
    tempresult = {}
    for key in newcondition:
        if key == value:
            pass
        else:
            tempresult[key] = newresult[key]
            recursion(newcondition[key], tempresult)

源码在我的博客上面：

TTyb