Louvain 论文笔记

Louvain

---

Introduce

Louvain算法是社区发现领域中经典的基于模块度最优化的方法，且是目前市场上最常用的社区发现算法。社区发现旨在发现图结构中存在的类簇（而非传统的向量空间）。

---

Algorithm Theory

• 模块度（modularity）

  要想理解Louvain算法需先理解模块度，模块度是衡量一个网络社区划分好坏的度量指标，可以简单理解为“给定算法得到的图中的社区划分D，社区内节点的连边权重和与对应随机图中的连边权重和的差，可以理解为社区内边权重之于社区间边权重的比例，当然，社区内边权重越大，则模块度越大，社区中节点联系更加紧密，社区划分质量越好。”模块度的公式如下所示：

  

  以下均无向无权图为例，m为图中的边数，2m为图的总度数，A为邻接矩阵，当两个节点直接相连时A_ij=1，否则A_ij=0，k_i为节点i的度，δ(c_i,c_j)为指示函数，当节点i、j位于同一个社区，其为1，否则为0。

  公式中比较难理解的是中括号中的第二项，啥意思呢？ 之前提到随机图，这边公式中的第二项指的是随机图中度为k_i和度为k_j的两个节点相连的概率。得到的社区划分与随机图（无规律，且无明显社区结构）相差越大，则社区内连接越紧密，社区间连接越稀疏（即社区边界更明显），发现的社区质量越好。

  好了，模块度就理解到这儿，简单总结一下，模块度范围在[-0.5,1)，一般模块度越高，发现的社区质量越好。（原始模块度论文表示当模块度值在0.3~0.7之间时，社区质量好）

• Louvain Flow Chart：

  现在进入正题，Louvain算法的总体框架（流程图）如下图所示：

  

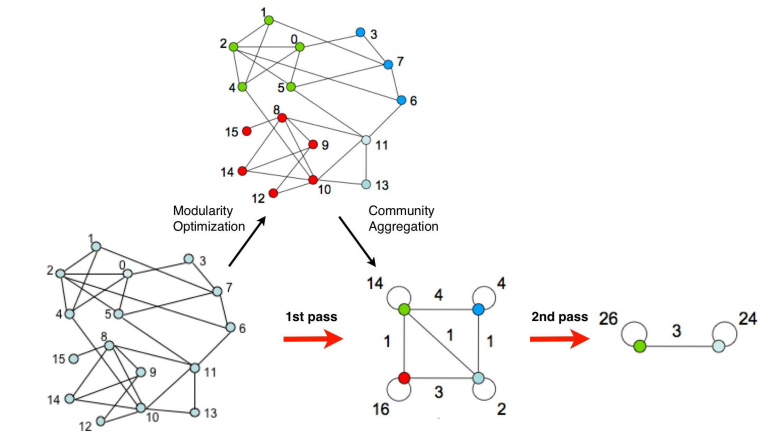
  Louvain是一个迭代更新算法（初始每个节点自成一个社区），每个迭代称为一个pass，每个pass都包括两个步骤。即Louvain算法等价于不断迭代以下两个步骤（阶段）：

  （1）步骤1：首先，为每个节点分配一个单独的社区。其次对于每个节点i，考虑其邻居j，计算将节点i归入节点j所在社区模块度的增益。考虑节点i的所有邻居，并且将节点i归入到模块度增益的社区最大。如果节点i归到他邻居所在社区都没有模块度增益（即模块度增益为0或者负数）的话，那节点i仍然留在他原始的社区中。这个过程反复做，直到改变任何节点的社区标签都没有更进一步的模块度增益就停止，停止之后第一阶段就结束了。以上最重要的就是要搞懂模块度增益这玩意怎么算呢？ 模块度增益可以通过以下公式计算。

  

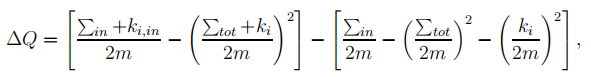
  啥意思呢？我们可以化简一下得到如下式子：

  \Delta Q =[\frac{k_{i,in}}{2m}-\frac{\sum_{tot}k_i}{2m^2}]
  

  括号中第一项的意思可以理解为节点i加入邻居所在社区之后对应社区内的连边数。括号中第二项的意思可以理解为结点加入邻居社区后，对应社区间以及社区内的连边数。最大化该模块度增益，就是最大化这个差，这个差大了，就说明节点i加入到这个邻居社区之后，使得该社区的内聚度更高了，社区结构越明显了。emmm，模块度增益最大化大概就是这么个意思了。

  （2）步骤2：算法的第二阶段做的事情是，结合步骤1得到的初始社区划分建立一个新的网络，新网络的节点是在第一阶段发现的初始社区（把社区粗化成一个粗化节点），两个粗化节点之间的边由两个社区原始对应的社区间边的权重和（无向图即两个社区间相连的边数），同一社区节点之间的连边权重生成这个社区粗化节点的一个自环边。一旦完成了第二阶段，就将构成的新的网络输入第一阶段再进行迭代（因为粗化（层次的概念），每次网络中的初始社区数会变小，因此后面迭代的速度会更快）。

  至此，Louvain算法介绍结束。

---

Reference

1. Blondel V D, Guillaume J L, Lambiotte R, et al. Fast unfolding of communities in large networks[J]. Journal of statistical mechanics: theory and experiment, 2008, 2008(10): P10008.
2. 社区发现算法——louvain完全解读
3. 模块度与Louvain社区发现算法