【数据结构与算法Python版学习笔记】树——相关术语、定义、实现方法

概念

一种基本的“非线性”数据结构——树

• 根
• 枝
• 叶

广泛应用于计算机科学的多个领域

• 操作系统
• 图形学
• 数据库
• 计算机网络

特征

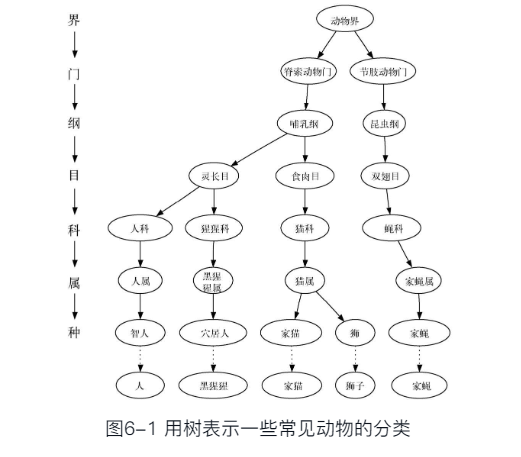
• 第一个属性是层次性，即树是按层级构建的，越笼统就越靠近顶部，越具体则越靠近底部。
• 第二个属性是，一个节点的所有子节点都与另一个节点的所有子节点无关。比如，猫属的子节点有家猫（英文名为Domestica）和狮。
• 第三个属性是，叶子节点都是独一无二的。

例子

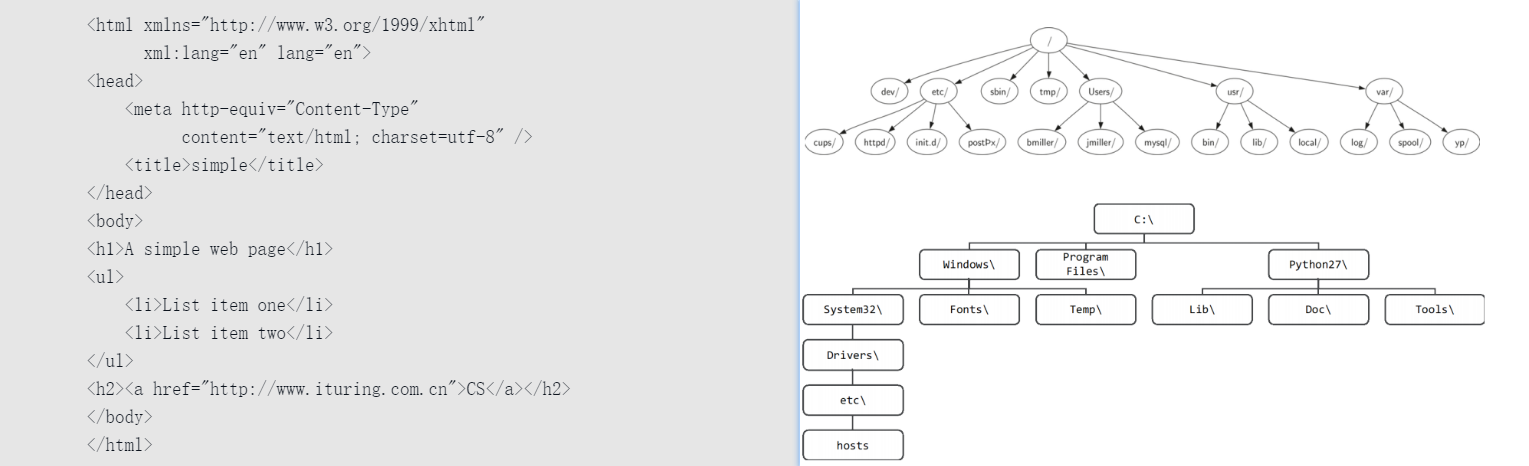
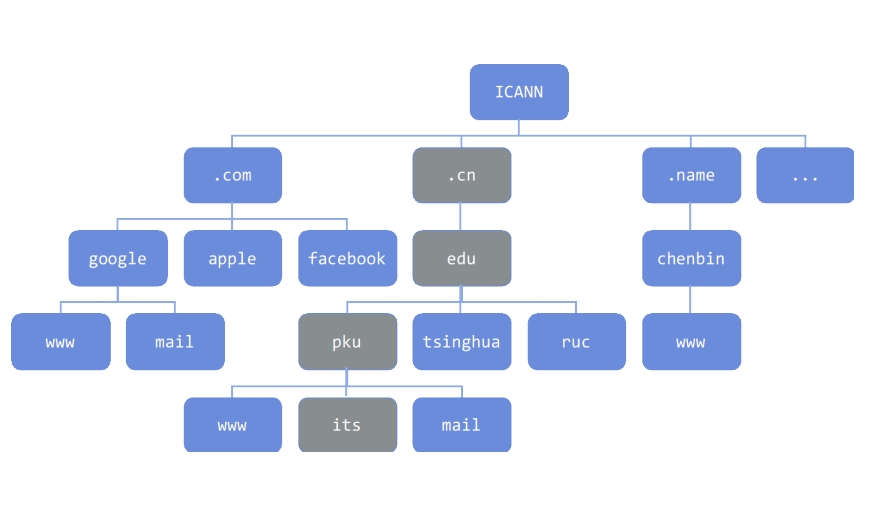
• 文件系统
• HTML文档（嵌套标记）
• 域名体系

---

术语

节点

• 节点是树的基础部分。
  
  它可以有自己的名字，我们称作“键”。节点也可以带有附加信息，我们称作“有效载荷”。有效载荷信息对于很多树算法来说不是重点，但它常常在使用树的应用中很重要。

边

• 边是树的另一个基础部分。
  
  两个节点通过一条边相连，表示它们之间存在关系。除了根节点以外，其他每个节点都仅有一条入边，出边则可能有多条。

根节点

• 根节点是树中唯一没有入边的节点。

路径

• 路径是由边连接的有序节点列表。
  
  比如，哺乳纲→食肉目→猫科→猫属→家猫就是一条路径。

子节点

• 一个节点通过出边与子节点相连。

父节点

• 一个节点是其所有子节点的父节点。

兄弟节点

• 具有同一父节点的节点互称为兄弟节点。

子树

• 一个父节点及其所有后代的节点和边构成一棵子树。

叶子节点

• 叶子节点没有子节点。

层数

• 节点n的层数是从根节点到n的唯一路径长度。
• 由定义可知，根节点的层数是0。

高度

• 树的高度是其中节点层数的最大值。

---

定义

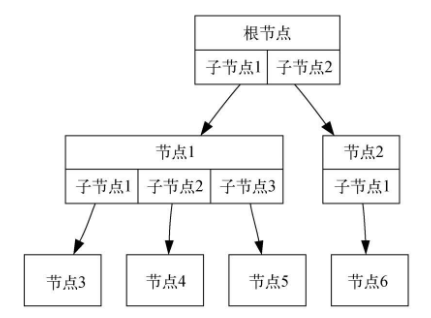
定义一：树由节点及连接节点的边构成。

树有以下属性：

• 有一个根节点；
• 除根节点外，其他每个节点都与其唯一的父节点相连；
• 从根节点到其他每个节点都有且仅有一条路径；
• 如果每个节点最多有两个子节点，我们就称这样的树为二叉树。

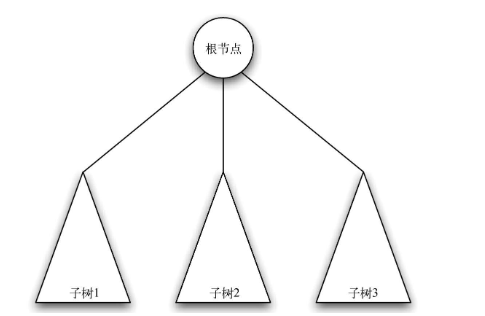
定义二（递归定义）

• 一棵树要么为空，要么由一个根节点和零棵或多棵子树构成，子树本身也是一棵树。每棵子树的根节点通过一条边连到父树的根节点。

---

实现

嵌套列表法

概念

• 用Python List来实现二叉树树数据结构
• 递归的嵌套列表实现二叉树， 由具有3个元素的列表实现：
  • 第1个元素为根节点的值；
  • 第2个元素是左子树（所以也是一个列表）；
  • 第3个元素是右子树（所以也是一个列表）。

优点

• 子树的结构与树相同，是一种递归数据结构
• 很容易扩展到多叉树，仅需要增加列表元素即可

函数

可以使用以下函数创建并操作二叉树。

• BinaryTree()创建一个二叉树实例。
• getLeftChild()返回当前节点的左子节点所对应的二叉树。
• getRightChild()返回当前节点的右子节点所对应的二叉树。
• setRootVal(val)在当前节点中存储参数val中的对象。
• getRootVal()返回当前节点存储的对象。
• insertLeft(val)新建一棵二叉树，并将其作为当前节点的左子节点。
• insertRight(val)新建一棵二叉树，并将其作为当前节点的右子节点。

# 树——嵌套列表法
def BinaryTree(r):
    return[r, [], []]

def insertLeft(root, newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1, [newBranch, t, []])
    else:
        root.insert(1, [newBranch, [], []])
    return root

def insertRight(root, newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2, [newBranch, [], t])
    else:
        root.insert(2, [newBranch, [], []])
    return root

def getRootValue(root):
    return root[0]

def setRootValue(root, newVal):
    root[0] = newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

if __name__ == "__main__":
    r = BinaryTree(3)
    insertLeft(r, 4)
    insertLeft(r, 5)
    insertRight(r, 6)
    insertRight(r, 7)
    l = getLeftChild(r)
    print(l)

    setRootValue(l, 9)
    print(r)
    insertLeft(l, 11)
    print(r)
    print(getRightChild(getRightChild(r)))

>>>
[5, [4, [], []], []]
[3, [9, [4, [], []], []], [7, [], [6, [], []]]]
[3, [9, [11, [4, [], []], []], []], [7, [], [6, [], []]]]
[6, [], []]

节点链接法

• 每个节点保存根节点的数据项，以及指向左右子树的链接

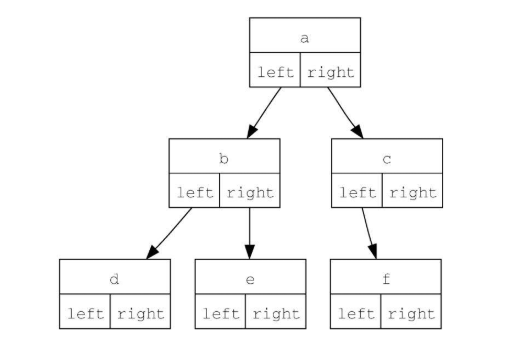
• 定义一个BinaryTree类
  • 成员key保存根节点数据项
  • 成员left/rightChild则保存指向左/右子树的引用（同样是BinaryTree对象）

# 节点链接法
class BinaryTree:
    def __init__(self,rootObj):
        self.key=rootObj
        self.leftChild=None
        self.rightChild=None

    def insertLeft(self,newNode):
        if self.leftChild==None:
            self.leftChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.leftChild=self.leftChild
            self.leftChild=t

    def insertRignt(self,newNode):
        if self.rightChild==None:
            self.rightChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.rightChild=self.rightChild
            self.rightChild=t

    def getRightChild(self):
        return self.rightChild

    def getLeftChild(self):
        return self.leftChild

    def setRootVal(self,obj):
        self.key=obj

    def getRootVal(self):
        return self.key

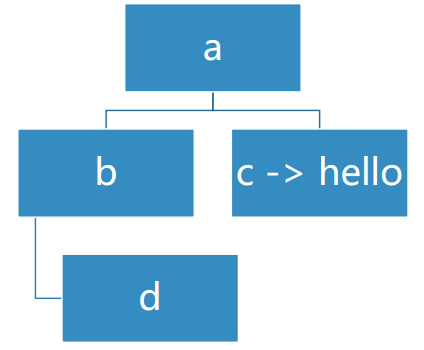
if __name__ == "__main__":
    r=BinaryTree('a')
    r.insertLeft('b')
    r.insertRignt('c')
    r.getRightChild().setRootVal('hello')
    r.getLeftChild().insertRignt('d')