【2020五校联考NOIP #7】道路扩建

题面传送门

题意：

给出一张 \(n\) 个点 \(m\) 条边的无向图 \(G\)，第 \(i\) 条边连接 \(u_i,v_i\) 两个点，权值为 \(w_i\)。

你可以进行以下操作一次：

• 选择两条边 \(i,j(i<j)\)，并令 \(w_i:=w_i+w_j\)。

求你可以得到的最短路的最大值。

\(n,m \in [1,3 \times 10^5]\)

很明显，你可以预处理出每条边的边权可以增加的最大值 \(add_i\)。

显然答案满足单调性，考虑二分答案。

需检查使得存在一条边 \(i\) 使得：

• 所有 \(1\) 到 \(n\) 的长度小于 \(mid\) 的路径都经过这条边。
• \(dis_{1,n}+add_i \geq mid\)。

检查第二个条件很好办，直接在原图上跑一遍最短路就可以了。

要检查第一个条件，可以将所有在至少一条 \(1\) 到 \(n\) 的长度小于 \(mid\) 的边全部拎出来建成一张新图 \(G'\)。

我们的目标就是找到 \(G'\) 中的一条边，把它割掉后 \(1\) 与 \(n\) 不连通。因为这样就不存在 \(1\) 到 \(n\) 的长度小于 \(mid\) 的路径。

可以使用 \(\texttt{tarjan}\) 找割边的方法找到这条边 \((u,v)\)。

但单纯地找割边也是不靠谱的，还需检查以下两个条件是否满足：

1. 它在点 \(1\) 与点 \(n\) 所在的连通块内。
2. \(1,n\) 不能全在点 \(u\) 或点 \(v\) 包含的连通块中。例如下图中 \((1,2)\) 就是反例：

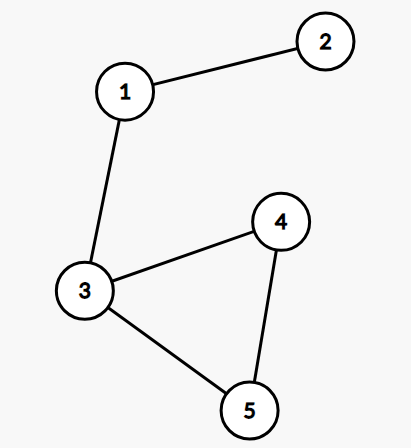
怎样检查这两个条件？

第一个条件很好办，从 \(1\) 开始 dfs，把能访问到的点都访问了就行了。

第二个条件等价于检查点 \(v\) 能否通过某条不包含 \((u,v)\) 的路径到达 \(n\)。你记录一个数组 \(vis_x\) 表示 \(x\) 能否到达 \(n\)。然后你每次访问一个未访问过的点的时候就执行 \(vis_x|=vis_y\) 就行了。

最后，聊一聊这题我调 3h 的原因：1. 没有注意到上面的条件 \(2\)，一直卡在 35 分（梦回 APIO？T2 调 2.5h 因为没考虑到某个条件） 2. 模板被错，if(low[y]>dfn[x]) 写成 if(low[y]>low[x])（说明模板最好考前敲一遍）。

/*
Contest: -
Problem: NFLSOJ 711
Author: tzc_wk
Time: 2020.10.19
*/
#include <bits/stdc++.h>
using namespace std;
#define fi			first
#define se			second
#define pb			push_back
#define fz(i,a,b)	for(int i=a;i<=b;i++)
#define fd(i,a,b)	for(int i=a;i>=b;i--)
#define foreach(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define all(a)		a.begin(),a.end()
#define fill0(a)	memset(a,0,sizeof(a))
#define fill1(a)	memset(a,-1,sizeof(a))
#define fillbig(a)	memset(a,0x3f,sizeof(a))
#define y1			y1010101010101
#define y0			y0101010101010
typedef pair<int,int> pii;
typedef long long ll;
int n,m,mx[300005];
int u[300005],v[300005],w[300005];
struct graph{
	int hd[300005<<1],nxt[300005<<1],to[300005<<1],wei[300005<<1],id[300005<<1],ecnt=0;
	inline void clear(){fill0(hd);fill0(to);fill0(wei);fill0(nxt);fill0(id);ecnt=0;}
	inline void adde(int u,int v,int w,int _id){to[++ecnt]=v;wei[ecnt]=w;id[ecnt]=_id;nxt[ecnt]=hd[u];hd[u]=ecnt;}
} g,ng;
ll dis1[300005],disn[300005];
inline void dijkstra(){
	priority_queue<pair<ll,int>,vector<pair<ll,int> >,greater<pair<ll,int> > > q;
	memset(dis1,63,sizeof(dis1));memset(disn,63,sizeof(disn));
	dis1[1]=disn[n]=0;q.push(make_pair(0,1));
	while(!q.empty()){
		pair<ll,int> p=q.top();q.pop();
		ll sum=p.fi;int x=p.se;
		if(dis1[x]<sum) continue;
		for(int e=g.hd[x];e;e=g.nxt[e]){
			int y=g.to[e],z=g.wei[e];
			if(dis1[y]>dis1[x]+z){
				dis1[y]=dis1[x]+z;
				q.push(make_pair(dis1[y],y));
			}
		}
	}
	q.push(make_pair(0,n));
	while(!q.empty()){
		pair<ll,int> p=q.top();q.pop();
		ll sum=p.fi;int x=p.se;
		if(disn[x]<sum) continue;
		for(int e=g.hd[x];e;e=g.nxt[e]){
			int y=g.to[e],z=g.wei[e];
			if(disn[y]>disn[x]+z){
				disn[y]=disn[x]+z;
				q.push(make_pair(disn[y],y));
			}
		}
	}
//	for(int i=1;i<=n;i++) printf("%lld ",dis1[i]);printf("\n");
//	for(int i=1;i<=n;i++) printf("%lld ",disn[i]);printf("\n");
}
int dfn[300005],low[300005],tim=0;
bool vis[300005],is[300005];vector<int> bri;
inline void tarjan(int x,int f){
	dfn[x]=low[x]=++tim;
	for(int e=ng.hd[x];e;e=ng.nxt[e]){
		int y=ng.to[e],z=ng.id[e];
		if(!dfn[y]){
			tarjan(y,x);low[x]=min(low[x],low[y]);vis[x]|=vis[y];
			if(low[y]>dfn[x]) is[z]=1;
		}
		else if(y!=f) low[x]=min(low[x],dfn[y]);
	}
	if(x==n) vis[x]=1;
}
inline bool check(ll x){
	ng.clear();
	memset(dfn,0,sizeof(dfn));memset(low,0,sizeof(low));
	memset(vis,0,sizeof(vis));tim=0;memset(is,0,sizeof(is));
//	for(int i=1;i<=m;i++) printf("%d\n",w[i]);
	for(int i=1;i<=m;i++){
		if(dis1[u[i]]+disn[v[i]]+w[i]<x||
		   disn[u[i]]+dis1[v[i]]+w[i]<x)
			ng.adde(u[i],v[i],1,i),ng.adde(v[i],u[i],1,i);
	}
	tarjan(1,0);if(!vis[1]) return 0;
	for(int i=1;i<=m;i++){
		ll d=min(dis1[u[i]]+disn[v[i]]+w[i],disn[u[i]]+dis1[v[i]]+w[i]);
//		if(is[i]) printf("%d %d %d %lld %lld\n",u[i],v[i],w[i],d+mx[i],d);
		if(vis[u[i]]&&vis[v[i]]&&is[i]&&d+mx[i]>=x) return 1;
	}
	return 0;
}
signed main(){
//	freopen("enlarge8.in","r",stdin);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u[i],&v[i],&w[i]);
		g.adde(u[i],v[i],w[i],i);g.adde(v[i],u[i],w[i],i);
	}
	for(int i=m;i;i--) mx[i]=max(w[i+1],mx[i+1]);
	dijkstra();ll L=dis1[n]+1,R=5e14,ans=dis1[n];
//	check(10);
	while(L<=R){
		ll mid=(L+R)>>1;
//		printf("%lld %d\n",mid,check(mid));
		if(check(mid)) ans=mid,L=mid+1;
		else R=mid-1;
	}
	printf("%lld\n",ans);
	return 0;
}