1.5.1- HTML之相对路径
网页需要图片,首先需要找到它。实际工作中,通常新建一个文件夹专门用于存放图像文件,这时插入图像,就需要采用“路径”的方式来制定图像文件的位置。路径可以分为相对路径与绝对路径。
相对路径
1.图像文件和HTML文件位于同一文件夹:只需输入图像文件的名称即可,如<img src="logo.gif">
2.图像文件位于HTML文件下一届文件夹,输入文件夹名和文件名,之间用“/”隔开,如<img src = "img/img01/logo.gif">。
3.图像文件位于HTML的上一级文件夹:在文件名之前加入“../”,如果是上两级,则需要使用“../../” ,依次类推,如<img src = "../logo.gif">。
同一级文件夹:
同一文件夹,存放HTML文件与图片可以直接调用,如图所示。

输入以下代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<img src="God father.jpg" alt="测试图片" /> </body>
</html>
在浏览器打开:
所以我们可以看出,HTML文件与图片在同一文件夹只需要输出文件名即可。
下一级文件夹
现在把刚才的那个文件放在同级文件夹images下。
这个时候如果HTML代码想找到插入这个图片需要输入这段代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<img src="data:images/God father.jpg" alt="测试图片" /> </body>
</html>
在浏览器打开:

我们可以同样找到这个图片,并在浏览器中显示。它是先找到了images文件架,然后再去找文件下面图片。 / 表示下一级。
上一级文件夹
我们这个时候把test.HTML放到与图片同级的HTML文件夹内:

这个时候我们的HTML文件怎么找到这个上一级的图片呢?输入以下代码:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<img src="../God father.jpg" alt="测试图片" /> </body>
</html>
在浏览器打开:

../代表上一级。
绝对路径
绝对路径:C:\Users\Administrator\Desktop\logo.gif。或完整的网络地址,例如:https://gss2.bdstatic.com/9fo3dSag_xI4khGkpoWK1HF6hhy/baike/s%3D220/sign=e11bef328a44ebf86971633de9f9d736/2fdda3cc7cd98d108b92da002c3fb80e7bec90b9.jpg
不管图片在什么地方,只需要右键点击图片,然后 点击属性,找到他的位置,然后复制下来就行,如图所示:
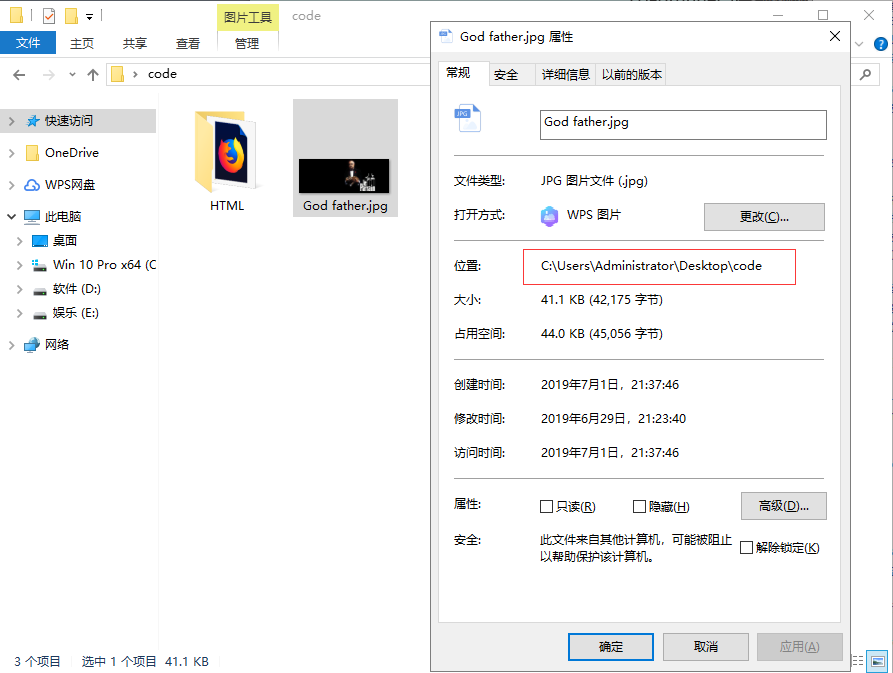
把这个图片路径复制下来,后面加上你的图名名称,然后代码如下:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<img src="C:\Users\Administrator\Desktop\God father.jpg" alt="测试图片" /> </body>
</html>
浏览器复制图片链接
代码如下:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Document</title>
</head>
<body>
<img src="https://ss1.baidu.com/6ONXsjip0QIZ8tyhnq/it/u=13264123,4092704128&fm=85&app=63&f=JPEG?w=121&h=75&s=0F64DA039CD205FDDE3CBD060100E091" alt="测试图片" /> </body>
</html>
浏览器打开如下:
1.5.1- HTML之相对路径的更多相关文章
- mapreduce中一个map多个输入路径
package duogemap; import java.io.IOException; import java.util.ArrayList; import java.util.List; imp ...
- Akka.net路径里的user
因为经常买双色球,嫌每次对彩票号麻烦,于是休息的时候做了个双色球兑奖的小程序,做完了发现业务还挺复杂的,于是改DDD重做设计,拆分服务,各种折腾...,不过这和本随笔没多大关系,等差不多了再总结一下, ...
- java中servlet的各种路径
1. web.xml中<url-pattern>路径,(叫它Servlet路径!) > 要么以“*”开关,要么为“/”开头 2. 转发和包含路径 > *****以“/”开头:相 ...
- 【C#代码实战】群蚁算法理论与实践全攻略——旅行商等路径优化问题的新方法
若干年前读研的时候,学院有一个教授,专门做群蚁算法的,很厉害,偶尔了解了一点点.感觉也是生物智能的一个体现,和遗传算法.神经网络有异曲同工之妙.只不过当时没有实际需求学习,所以没去研究.最近有一个这样 ...
- 使用JavaScript为一张图片设置备选路径
在做网页开发的时候,有时候希望给图片设置一个备选路径,即,当src属性对应的主路径加载失败的时候,图片可以马上切换到备选路径.这样,即使主路径失效了,显示备用路径也不会影响网页的正常体验. 注意到网页 ...
- iOS之开发中一些相关的路径以及获取路径的方法
模拟器的位置: /Applications/Xcode.app/Contents/Developer/Platforms/iPhoneSimulator.platform/Developer/SDKs ...
- Android中访问sdcard路径的几种方式
以前的Android(4.1之前的版本)中,SDcard路径通过"/sdcard"或者"/mnt/sdcard"来表示,而在JellyBean(安卓4.1)系统 ...
- 【每日一linux命令1】linux命令路径
一.路径: 执行命令前必须要考虑的一步是命令的路径,若是路径错误或是没有正确的指定,可能导致错误 的执行或是找不到该命令.要知道设置的路径,可执行以下命令: echo $PATH 显示结果: 这时我们 ...
- hibernate-mapping-3.0.dtd;hibernate-configuration-3.0.dtd;hibernate.properties所在路径
hibernate-mapping-3.0.dtd 所在路径:hibernate-release-5.2.5.Final\project\hibernate-core\src\main\resourc ...
- .NET全栈开发工程师学习路径
PS:最近一直反复地看博客园以前发布的一条.NET全栈开发工程师的招聘启事,觉得这是我看过最有创意也最朴实的一个招聘启事,更为重要的是它更像是一个技术提纲,能够指引我们的学习和提升,现在转载过来与各位 ...
随机推荐
- Java 基础加强 02
基础加强·反射 和 枚举 类的加载概述和加载时机 * A:类的加载概述 * 当程序要使用某个类时,如果该类还未被加载到内存中,则系统会通过加载.连接.初始化来实现对这个类的初始化 * 加载 * 就是指 ...
- #String类简述(小白理解,小白编写,欢迎大神指点,小白跪谢)
@ 目录 一.前言(可忽略) 二.String变量的认知 三.String类的构造方法 四.String类的基本方法 4.1 toString()方法 4.2 equals()方法 4.3 equal ...
- Java 并发编程小册整理好了
Java 有并发,并发知识之大,一口吃不下 这曾是我不愿意触碰的知识角 多次一头扎进并发,无功而返 为应对面试,临时苦苦记忆,不成体系 这一次我决定从基础开始,攻克它 12,0000 字 68Mb 高 ...
- 实话实说:只会.NET,会让我们一直处于鄙视链、食物链的下游
金三银四,是个躁动的季节. 结合最近的面试,谈一谈一个老牌开发人员的面试感悟. 大家都知道我的主力技术栈是 .NET + Devops + 弱前端 (当前技术认知,不排除以后变化). 面试了大小厂,有 ...
- 顺序表及基本操作(C语言)
#include <stdio.h> #include <stdlib.h> //基本操作函数用到的状态码 #define TRUE 1; #define FALSE 0; # ...
- PTE 准备之 Personal introduction
Task strategies Be prepared! This is your opportunity to give the admissions officers a first impres ...
- python-顺序队列的实现
class seqqueue(object): 8 def __init__(self,maxsize): 9 self.maxsize = maxsize 10 self.queueelem = [ ...
- The 2018 ACM-ICPC CCPC NING XIA G-Factories
题意:在一棵数的叶子上建k个工厂保证,求两两距离之和的最小值. 思路:如果一个一个叶子节点去考虑去与否太麻烦了,直接考虑该节点的子树上选取几个作为工厂,利用树形DP,dp[u][i]表示的是u节点为根 ...
- Angle Beats Gym - 102361A
题目链接:https://vjudge.net/problem/Gym-102361A 题意:给定N个点,q次询问每次询问给一个点,问在N个点中取2个和给定点最多可以组成几个直角三角形. 思路:htt ...
- P1208 [USACO1.3]混合牛奶 Mixing Milk(JAVA语言)
思路 按单价排序然后贪心 题目描述 由于乳制品产业利润很低,所以降低原材料(牛奶)价格就变得十分重要.帮助Marry乳业找到最优的牛奶采购方案. Marry乳业从一些奶农手中采购牛奶,并且每一位奶农为 ...
