Solution -「CF 1375G」Tree Modification

\(\mathcal{Description}\)

  Link.

  给定一棵 \(n\) 个结点的树，每次操作选择三个结点 \(a,b,c\)，满足 \((a,b),(b,c)\in E\)，并令 \(a\) 的所有邻接点（包括 \(b\)）与 \(c\) 邻接且不再与 \(a\) 邻接；再令 \(a\) 与 \(c\) 邻接。求至少几次操作使树变为菊花图。

  \(n\le2\times10^5\)。

  操作图例：

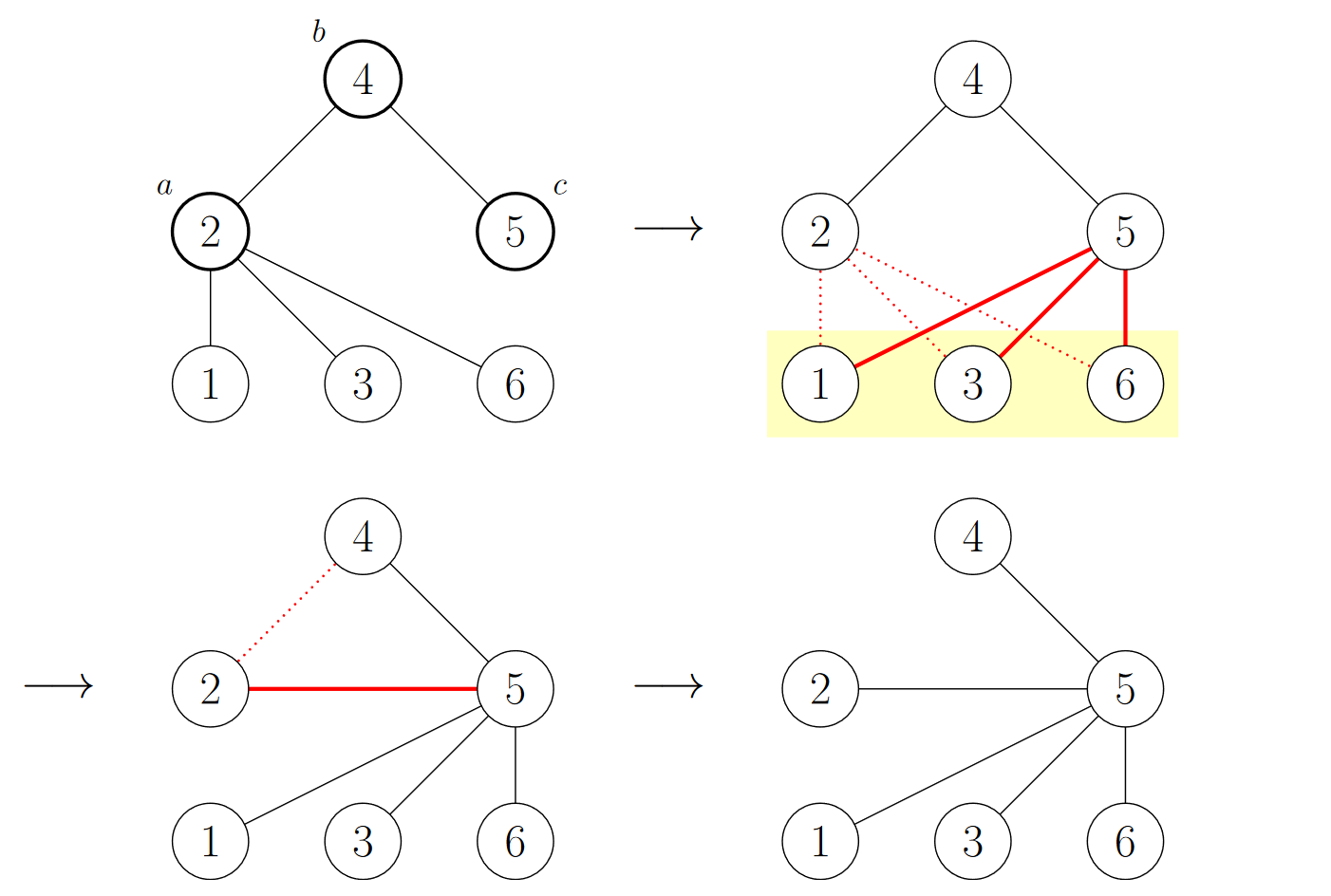
\(\mathcal{Solution}\)

  和 CF1025G 有点类似。不妨令 \(1\) 为树的根，结点 \(u\) 的深度记为 \(d(u)\)，\(d(1)=1\)。构造势能函数 \(\Phi:T\rightarrow\mathbb N_+\)，有：

\[\Phi(T)=\sum_{u\in T}[2|d(u)]
\]

  先考虑目标状态，菊花图的势能显然为 \(1\)（根是花瓣）或 \(n-1\)（根是花蕊）。再观察一次操作带来的势能变化，发现仅有 \(a\) 结点的深度的奇偶性改变，那么：

\[\Delta\Phi=\pm1
\]

  记初始时树为 \(S\)，可知答案为：

\[\min\{(n-1)-\Phi(S),\Phi(S)-1\}
\]

  复杂度 \(\mathcal O(n)\)。嗯唔，做完了 www！

\(\mathcal{Code}\)

/* Clearink */

#include <cstdio>

inline int rint () {
	int x = 0, f = 1; char s = getchar ();
	for ( ; s < '0' || '9' < s; s = getchar () ) f = s == '-' ? -f : f;
	for ( ; '0' <= s && s <= '9'; s = getchar () ) x = x * 10 + ( s ^ '0' );
	return x * f;
}

template<typename Tp>
inline void wint ( Tp x ) {
	if ( x < 0 ) putchar ( '-' ), x = ~ x + 1;
	if ( 9 < x ) wint ( x / 10 );
	putchar ( x % 10 ^ '0' );
}

const int MAXN = 2e5;
int n, ecnt, head[MAXN + 5], cnt[2];

struct Edge { int to, nxt; } graph[MAXN * 2 + 5];

inline void link ( const int s, const int t ) {
	graph[++ ecnt] = { t, head[s] };
	head[s] = ecnt;
}

inline void solve ( const int u, const int f, const int dep ) {
	++ cnt[dep & 1];
	for ( int i = head[u], v; i; i = graph[i].nxt ) {
		if ( ( v = graph[i].to ) ^ f ) {
			solve ( v, u, dep + 1 );
		}
	}
}

int main () {
	n = rint ();
	for ( int i = 1, u, v; i < n; ++ i ) {
		u = rint (), v = rint ();
		link ( u, v ), link ( v, u );
	}
	solve ( 1, 0, 0 );
	printf ( "%d\n", ( cnt[0] < cnt[1] ? cnt[0] : cnt[1] ) - 1 );
	return 0;
}

\(\mathcal{Details}\)

  势能分析的方法有点像数学上的特征值法。这种操作题没思路的时候不妨研究一下单次操作，构造出一个变化极为简单的“特征”来快速求解。