两圆相交求面积 hdu5120

转载

两圆相交分如下集中情况：相离、相切、相交、包含。

设两圆圆心分别是O1和O2，半径分别是r1和r2，设d为两圆心距离。又因为两圆有大有小，我们设较小的圆是O1。

相离相切的面积为零，代码如下：

1. double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
2. if (d >= r1+r2)
3. return 0;

double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
if (d >= r1+r2)
	return 0;

包含的面积就是小圆的面积了，代码如下：

1. if(r2 - r1 >= d)
2. return pi*r1*r1;

if(r2 - r1 >= d)
	return pi*r1*r1;

接下来看看相交的情况。

相交面积可以这样算：扇形O1AB - △O1AB + 扇形O2AB - △O2AB，这两个三角形组成了一个四边形，可以用两倍的△O1AO2求得，

所以答案就是两个扇形-两倍的△O1AO2

因为

所以

那么

同理

接下来是四边形面积：

代码如下：

double ang1=acos((r1*r1+d*d-r2*r2)/(*r1*d));
double ang2=acos((r2*r2+d*d-r1*r1)/(*r2*d));
return ang1*r1*r1 + ang2*r2*r2 - r1*d*sin(ang1);

#include<iostream>
#include<cmath>
using namespace std;

#define pi acos(-1.0)

typedef struct node
{
    int x;
    int y;
}point;

double AREA(point a, double r1, point b, double r2)
{
    double d = sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
    if (d >= r1+r2)
        return ;
    if (r1>r2)
    {
        double tmp = r1;
        r1 = r2;
        r2 = tmp;
    }
    if(r2 - r1 >= d)
        return pi*r1*r1;
    double ang1=acos((r1*r1+d*d-r2*r2)/(*r1*d));
    double ang2=acos((r2*r2+d*d-r1*r1)/(*r2*d));
    return ang1*r1*r1 + ang2*r2*r2 - r1*d*sin(ang1);
}

int main()
{
    point a, b;
    a.x=, a.y=;
    b.x=, b.y=;
    double result = AREA(a, , b, );
    printf("%lf\n", result);
    return ;
}

Intersection

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 3443    Accepted Submission(s): 1302

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.

A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.

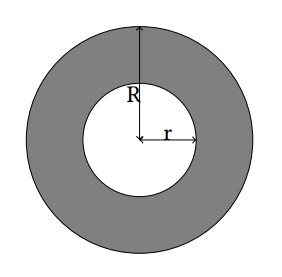
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

Input

The first line contains only one integer T (T ≤ 10⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x_i, y_i (0 ≤ x_i, y_i ≤ 20) indicating the coordinates of the center of each ring.

 

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

Sample Input

2

2 3

0 0

0 0

2 3

0 0

5 0

 

Sample Output

Case #1: 15.707963

Case #2: 2.250778

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
double x1,ya,x2,y2,dis,s1,s2,s3,R,r;
double sov(double R,double r){
    if(dis>=r+R) return ;
    if(dis<=R-r) return acos(-1.0)*r*r;
    double x=(R*R-r*r+dis*dis)/2.0/dis;
    double y=(r*r-R*R+dis*dis)/2.0/dis;
    double seta1=*acos(x/R);
    double seta2=*acos(y/r);
    double ans=seta1*R*R/2.0+seta2*r*r/2.0;
    double h=sqrt(R*R-x*x);
    return ans-dis*h;
}
int main(){
   int tas=,T;
   for(scanf("%d",&T);T--;){
    scanf("%lf%lf",&r,&R);
    scanf("%lf%lf%lf%lf",&x1,&ya,&x2,&y2);
    dis=sqrt((x1-x2)*(x1-x2)+(ya-y2)*(ya-y2));
    s1=sov(R,R),s2=sov(R,r),s3=sov(r,r);
    printf("Case #%d: %.6f\n",tas++,s1-*s2+s3);
   }
}