广义线性模型|logistics|Odds ratio|最大似然函数|LR|AIC|

广义线性模型

y是分类变量

Link function:将分类变量和数值变量放在一起

使用得到结果0 or 1的概率值来评估选0 or1

函数关系：

正比例函数：

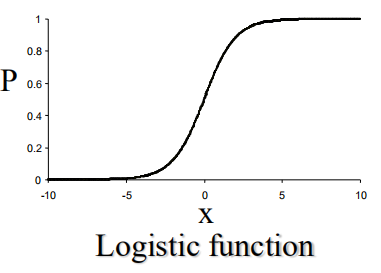
logistics函数S型曲线：

Odds ratio反应事件发生的倾向性

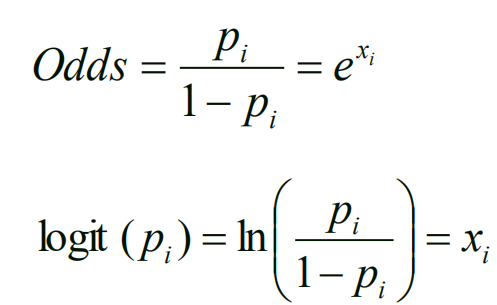
logistics函数与probit regression function很像，但是logistics函数基于二项分布，probit regression function基于正态分布。

probit regression function：正态分布的累计概率曲线

logistics函数不需要独立+方差齐性+正态性。

p是怎么根据x变化的，求其偏导：

其中，α和β由之前的数据给定，由最大似然估计确定。

正态分布用样本估计总体，取两个点测试不同的假设均值，找到使得似然函数最大，具体就是列出似然函数对μ求导，令导数为零，即找到最大值。以此类推，可以取n个点。求方差也是同理，对SD求导。

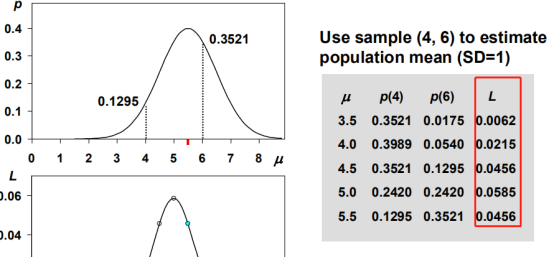
最终结果是，

按照以上思路，而不是反求思路得到的图像是：

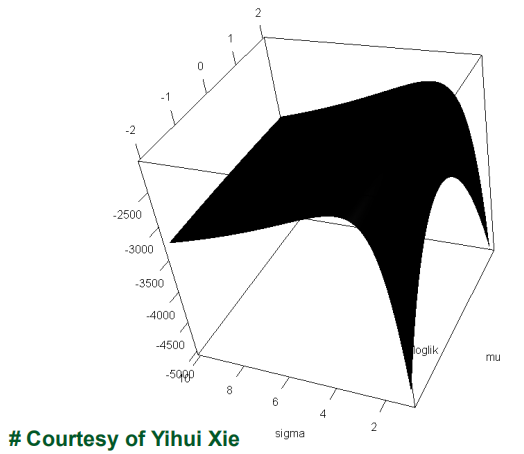
必须是总体正态分布，使用MLE估计参数，此时与最小二乘法等同。如果不是正态分布，则不同。

ANOVA, Pearson’s r, t-test, regression

使用广义线性模型得到的概率，将该概率放回原始数据中，计算其差值，该差值符合卡方分布。LR

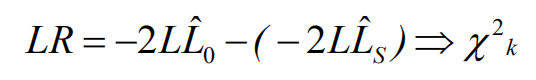
评价拟合优度的指标：

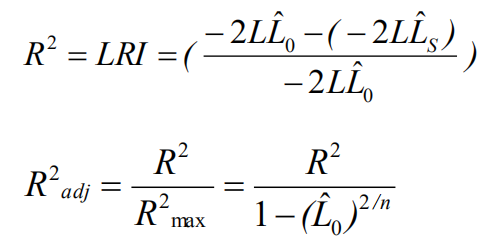
AIC在相同数目的变量解释同一变量时才会有可比性。越小越好。

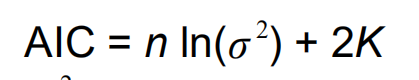
K的选择：如果增大K值是使得likehood变化很大，就要可取，但是如果增大K值是使得likehood变化很小，就不可取。

对于小数据，少于40，扁平化数据，没有充分的重复来解释规律，所以引入了一个修正。修改原始数据量的方法是扩大n减小k。