GeoGebra案例(傅里叶级数的方波)
傅里叶级数介绍:请移步参见这位马大佬的博文
https://www.matongxue.com/madocs/619.html
马大佬中的gif图在我看来是非常直观且有趣的,奈何本人本领实在有限,学习不精,所以从GeoGebra上找了一个方波案例先来分享一下。
链接如下
链接:https://pan.baidu.com/s/1EbMif1ErxXxs0afyJCOiaA
提取码:9zfy
案例中的指令如下:
1、Even = Sum(Sequence(Element(a, n) cos(n k x), n, 1, N))
2、Fourier = a0 + Even(x) + Odd(x)
3、Odd = Sum(Sequence(Element(b, n) sin(n k x), n, 1, N))
4、If(x < 0, 0, 3)
5、a = Sequence(2 / p Integral(f(x) cos(n k x), xa, xb), n, 1, 25)
6、b = Sequence(2 / p Integral(f(x) sin(n k x), xa, xb), n, 1, 25)
7、N= 25
8、N_{max} = 30
9、a0=1 / p Integral(f, xa, xb)
10、k = 1
11、p = 6.28
12、xa = -3.14159
13、xb = π

案例中的结果如下:
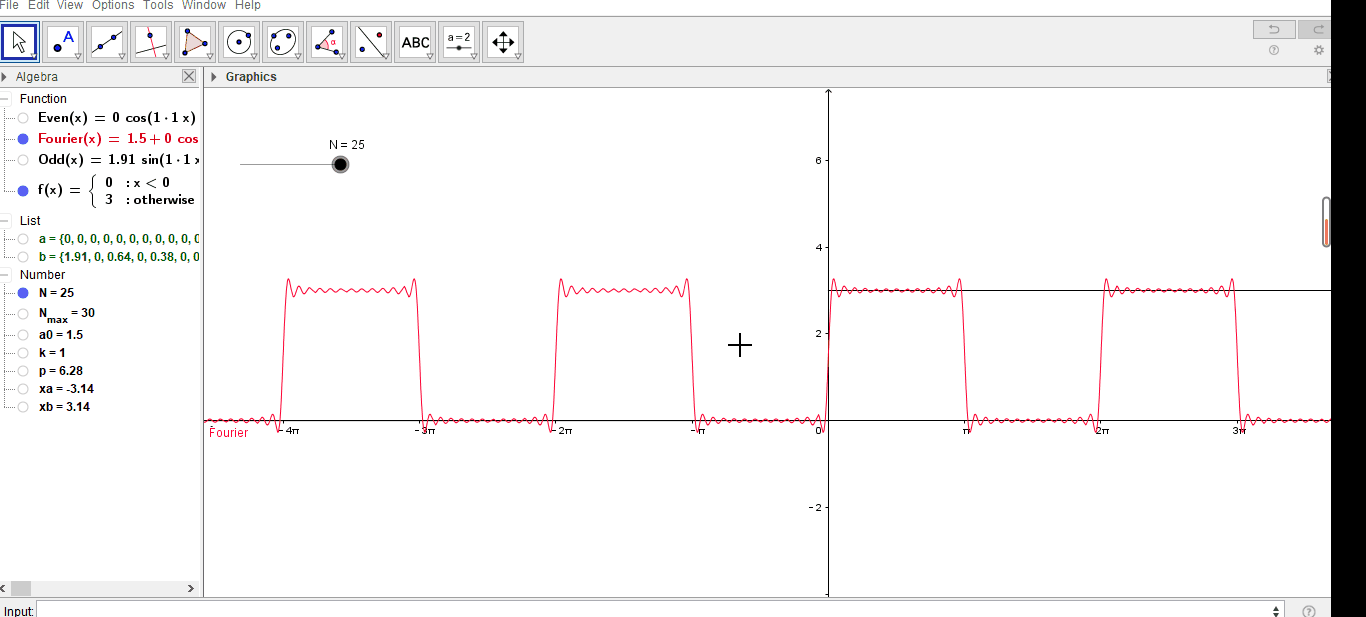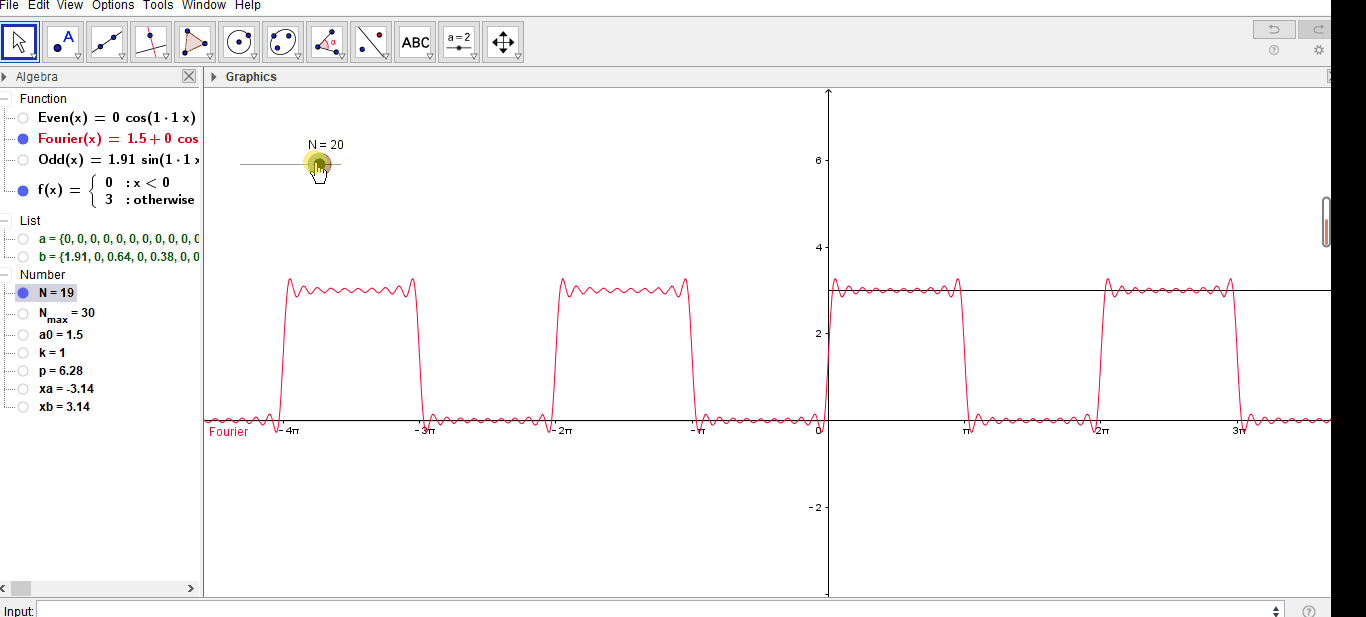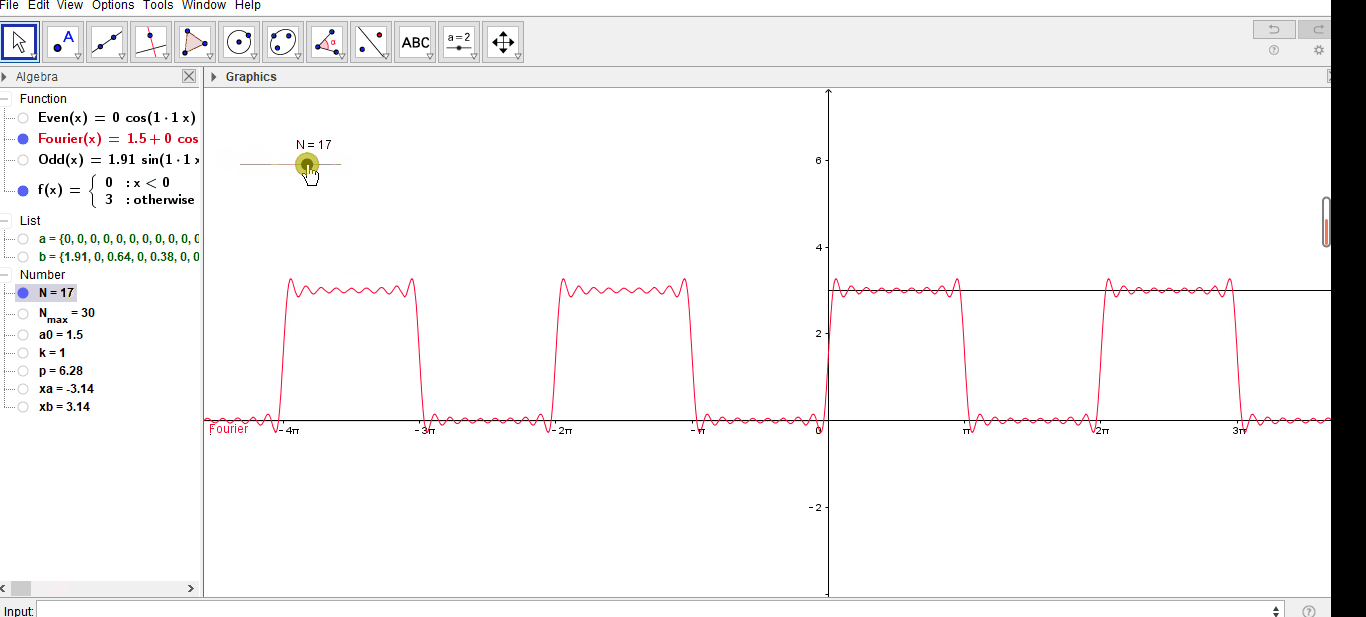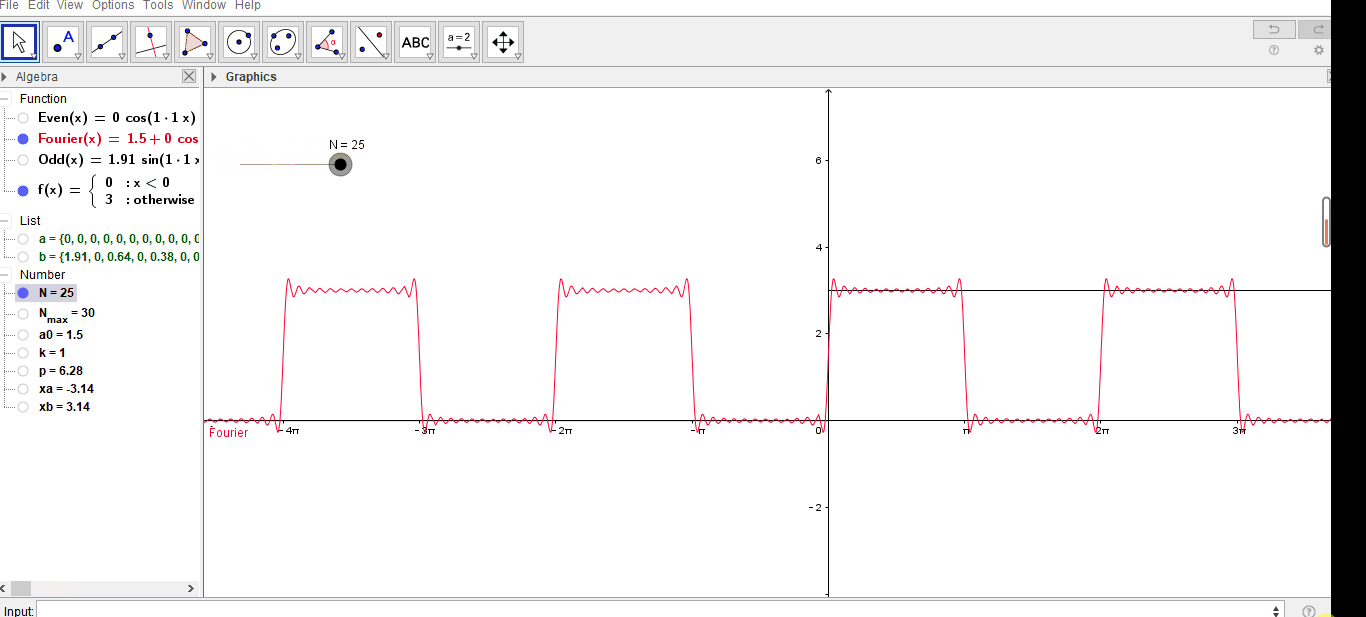
GeoGebra案例(傅里叶级数的方波)的更多相关文章
- GeoGebra学习-lesson1
我曾经想过学习数学的时候总觉得不太直观,希望通过直观的图形来直观的学习数学.庆幸的是,在B站看视频时看到了妈咪叔使用了这款数学软件,很好用的样子.就去简单的了解了一下,下面是摘抄自<Geogeb ...
- STM32单片机应用与全案例实践 /stm32自学笔记 第二版 pdf
STM32单片机应用与全案例实践pdf https://pan.baidu.com/s/16WrivuLcHvLTwS__Zcwl6Q 4rj3 stm32自学笔记 第二版 pdf https://p ...
- 数据库优化案例——————某市中心医院HIS系统
记得在自己学习数据库知识的时候特别喜欢看案例,因为优化的手段是容易掌握的,但是整体的优化思想是很难学会的.这也是为什么自己特别喜欢看案例,今天也开始分享自己做的优化案例. 最近一直很忙,博客产出也少的 ...
- SQL Server内存遭遇操作系统进程压榨案例
场景: 最近一台DB服务器偶尔出现CPU报警,我的邮件报警阈(请读yù)值设置的是15%,开始时没当回事,以为是有什么统计类的查询,后来越来越频繁. 探索: 我决定来查一下,究竟是什么在作怪,我排查的 ...
- solr_架构案例【京东站内搜索】(附程序源代码)
注意事项:首先要保证部署solr服务的Tomcat容器和检索solr服务中数据的Tomcat容器,它们的端口号不能发生冲突,否则web程序是不可能运行起来的. 一:solr服务的端口号.我这里的sol ...
- Yeoman 官网教学案例:使用 Yeoman 构建 WebApp
STEP 1:设置开发环境 与yeoman的所有交互都是通过命令行.Mac系统使用terminal.app,Linux系统使用shell,windows系统可以使用cmder/PowerShell/c ...
- 了不起的 nodejs-TwitterWeb 案例 bug 解决
了不起的nodejs算是一本不错的入门书,不过书中个别案例存在bug,按照书中源码无法做出和书中相同效果,原本兴奋的心情掺杂着些许失落. 现在我们看一下第七章HTTP,一个Twitter Web客户端 ...
- 一个表缺失索引发的CPU资源瓶颈案例
背景 近几日,公司的应用团队反应业务系统突然变慢了,之前是一直比较正常.后与业务部门沟通了解详情,得知最近生意比较好,同时也在做大的促销活动,使得业务数据处理的量出现较大的增长,最终系统在处理时出现瓶 ...
- 【Machine Learning】决策树案例:基于python的商品购买能力预测系统
决策树在商品购买能力预测案例中的算法实现 作者:白宁超 2016年12月24日22:05:42 摘要:随着机器学习和深度学习的热潮,各种图书层出不穷.然而多数是基础理论知识介绍,缺乏实现的深入理解.本 ...
随机推荐
- Django之Ajax传输数据
MTV与MVC模型 MTV与MVC都是模型,只不过MTV是django自己定义的,具体看一下他们的意思 MTV模型(django) M:模型层(models.py) T:templates文件夹 V: ...
- select_related prefetch_related
# select_related与prefetch_related# # select_related帮你直接连表操作 查询数据 括号内只能放外键字段# # res = models.Book.obj ...
- MRCTF 部分WriteUp
前言 周末做了一下北邮的CTF,这里记录一下做出来的几道题.(PS:比较菜有很多没做出来 >_< ,还是要更加努力学习啊(ง •̀o•́)ง,剩下的等大佬们出了wp后在复现一下) Web ...
- effective-java学习笔记---使用枚举类型替代整型常量34
1.要将数据与枚举常量相关联,请声明实例属性并编写一个构造方法,构造方法带有数据并将数据保存在属性中. // Enum type with data and behavior public enum ...
- PHP一致性hash
PHP提供了两种比较两个变量的方法: 松散比较使用 == or != : 两个变量都具有“相同的值”. 严格比较 === or !== : 两个变量都具有“相同的类型和相同的值”. 类型杂耍 真实陈述 ...
- 技术大佬:我去,你竟然还在用 try–catch-finally
二哥,你之前那篇 我去 switch的文章也特么太有趣了,读完后意犹未尽啊,要不要再写一篇啊?虽然用的是 Java 13 的语法,对旧版本不太友好.但谁能保证 Java 不会再来一次重大更新呢,就像 ...
- Spring 事务注意事项
使用事务注意事项 1,事务是程序运行如果没有错误,会自动提交事物,如果程序运行发生异常,则会自动回滚. 如果使用了try捕获异常时.一定要在catch里面手动回滚. 事务手动回滚代码 Transact ...
- JVM tomcat 性能调优
1,新建web 测试项目并且发布到Tomcat,访问路径:http://127.0.0.1:8080/JvmWeb/index @WebServlet("/index") publ ...
- Activiti任务分配
分配任务负责人 一.固定分配 在进行业务流程建模时指定固定的任务负责人 在properties 视图中,填写Assignee 项为任务负责人. 注意: 由于固定分配方式,任务只管一步一步执行任务,执行 ...
- storm学习初步
本文根据自己的了解,对学习storm所需的一些知识进行汇总,以备之后详细了解. maven工具 参考书目 Maven权威指南 官方文档 Vagrant 分布式开发环境 博客 storm 参考书目 Ge ...
