UVA - 12113 Overlapping Squares（重叠的正方形）

题意：给定一个4*4的棋盘和棋盘上所呈现出来的纸张边缘，问用不超过6张2*2的纸能否摆出指定的形状。

分析：2*2的纸在4*4的棋盘上总共有9种放置位置，枚举所有的放置位置即可。枚举情况总共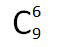种。

#pragma comment(linker, "/STACK:102400000, 102400000")
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<cmath>
#include<iostream>
#include<sstream>
#include<iterator>
#include<algorithm>
#include<string>
#include<vector>
#include<set>
#include<map>
#include<stack>
#include<deque>
#include<queue>
#include<list>
#define Min(a, b) ((a < b) ? a : b)
#define Max(a, b) ((a < b) ? b : a)
typedef long long ll;
typedef unsigned long long llu;
const int INT_INF = 0x3f3f3f3f;
const int INT_M_INF = 0x7f7f7f7f;
const ll LL_INF = 0x3f3f3f3f3f3f3f3f;
const ll LL_M_INF = 0x7f7f7f7f7f7f7f7f;
const int dr[] = {0, -1, 0, 1, -1, -1, 1, 1};//西北东南
const int dc[] = {-1, 0, 1, 0, -1, 1, -1, 1};
const int MOD = 1e9 + 7;
const double pi = acos(-1.0);
const double eps = 1e-15;
const int MAXN = 10 + 10;
const int MAXT = 10000 + 10;
using namespace std;
char pic[MAXN][MAXN];
char p1[MAXN][MAXN];
int vis[MAXN];
bool judge(){//判断是否摆成目标形状
    for(int i = 0; i < 5; ++i){
        for(int j = 0; j < 9; ++j){
            if(pic[i][j] != p1[i][j]) return false;
        }
    }
    return true;
}
bool dfs(int step){
    if(judge()) return true;
    if(step >= 6) return false;
    char p2[MAXN][MAXN];
    memcpy(p2, p1, sizeof p1);//p2便于恢复p1数组内容
    for(int i = 0; i < 9; ++i){//枚举2*2正方形可以放置的9个位置
        if(!vis[i]){
            vis[i] = 1;
            int r = i / 3;
            int c = 2 * (i % 3) + 1;
            p1[r][c] = p1[r][c + 2] = p1[r + 2][c] = p1[r + 2][c + 2] = '_';
            p1[r + 1][c - 1] = p1[r + 2][c - 1] = p1[r + 1][c + 3] = p1[r + 2][c + 3] = '|';
            p1[r + 1][c] = p1[r + 1][c + 1] = p1[r + 1][c + 2] = p1[r + 2][c + 1] = ' ';
            if(dfs(step + 1)) return true;
            vis[i] = 0;
            memcpy(p1, p2, sizeof p1);
        }
    }
    return false;
}
int main(){
    int kase = 0;
    while(gets(pic[0]) != NULL){
        if(pic[0][0] == '0') return 0;
        memset(vis, 0, sizeof vis);
        for(int i = 1; i < 5; ++i){
            gets(pic[i]);
        }
        printf("Case %d: ", ++kase);
        for(int i = 0; i < 5; ++i){
            for(int j = 0; j < 9; ++j){
                p1[i][j] = ' ';
            }
        }
        if(dfs(0)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}