03_K近邻算法

　　今天是2020年2月1日星期六，疫情延续，现在确诊人数达到了11821例，艰难困苦，玉汝于成，相信国家的力量！大家齐心协力干一件事，疫情会尽早结束的，武汉加油。前几天整理感知机算法的内容，发现写博客这件事情，的确是有利于学习啊，把知识点写出来，自己心里得对内容十分清楚。动手去做这件事情真的是太重要了，知道做不到等于不知道啊。现在记录的算是初稿，先把三分之一的内容整理出来，开学再详细整理，再确认几遍后，再发表到博客上。反反复复的这几遍，相当于反反复复的理解知识点，书读百遍其义自见，知识点想不明白也该明白了。争取开学前把监督学习部分的原理讲解部分弄完，开学一个月左右的时间完成二次学习整理，坚持下来的话，暑假前完成该书的学习。理想很丰满~加油~

---

GitHub:https://github.com/wangzycloud/statistical-learning-method

---

K近邻算法

引入

　　首先K近邻算法是一种基本的分类与回归方法，这里只讨论分类问题中的K近邻法。顾名思义，近邻算法要根据某实例点附近的情况，判断该实例点的类别，也就是找到该实例点附近的几个实例，看看它们都属于什么类别，然后确定该实例点所属的类别。

　　这是具有实际意义的，举个感冒病人是否需要输液的例子，病情严重的病人，发热乏力咳嗽的症状是严重的，病情严重的群体，大家发热乏力咳嗽的症状是类似的，具有体温高的症状，或者具有流鼻涕的症状，或者具有咳嗽的症状，这部分群体具有相似的特征；同样，没有病情的群体，各项症状是正常的，不会有体温高、咳嗽、乏力这些症状（在这里不考虑其它疾病是否导致这些症状）。那么，对于一个新的来诊人员B，若具有了上述症状，体温和需要输液的患者A一样高，和患者A同样具有咳嗽、乏力等症状。在特征的表现上，B和A具有了非常高的相似性，那么，我们就可以根据这些相似的症状，判断B需要输液了。对于新的来诊人员C，若C不具有体温高、咳嗽乏力等症状，和患者A的相似性差距很大，那么就没有理由判断C是一个感冒病人。我们可以通过C具有的病症特征（和哪些病人情况相似），判断C患有什么疾病，属于什么分类。

　　如何衡量“附近”？如何衡量相似性？这叫距离度量。需要找到多少症状相似的患者？这叫K值的选择。找到了K个症状相似的患者，如何判断新患者的疾病？根据K个病人的症状判断新患者的疾病，这叫分类决策规则。

　　K近邻法假设给定一个训练数据集，其中的实例类别已经确定，将输入空间的实例点映射到特征空间，用特征向量作为输入，输出实例的类别。分类时，根据k个最近邻的训练实例的类别，通过多数表决等方式进行预测。

　　可以看到，K近邻法不具有显式的学习过程，实际上是对特征空间的划分，利用训练数据，将特征向量空间划分为不同子区域，新的实例点根据相似性找到所属区域，作为分类的“模型”。接下来将按照书中讲述的次序，学习K近邻算法、模型、三要素及kd树。

K近邻算法

　　K近邻算法简单、直观。给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于哪个类，就把该输入实例划分到这个类中。

　　算法流程图：

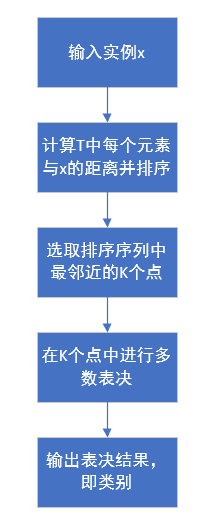
　　K=1时，称为最近邻算法，对于输入的实例点x，将训练集中最近邻点的类别作为x的类别。

K近邻模型

　　上文提到，K近邻模型实际上对应于特征空间的划分，由三个基本要素构成，距离度量、K值的选择和分类决策规则。K近邻模型对于一个新的输入实例，它所属的类别被唯一的确定，这相当于根据该实例的特征表现，将特征空间划分为一些子空间，确定子空间中每个实例点所属的类别。

　　在现实场景中，对于要分类的数据，数据与数据之间具有相似性是被分类的依据，物以类聚是指同样的东西才能聚在一起，相互关联关系比较近，才可以被归为一类。先把输入实例映射到特征空间，找到可以表征实例的特征向量，对每个训练实例点x，距离该点比其它点更近的所有点组成一个区域，叫做单元，每个训练实例点属于一个单元，所有单元将特征空间划分为各个子部分，每个单元中实例点的类别都是确定的。

1)距离度量

　　特征空间中两个实例点的距离是两个实例点相似程度的反映，在特征空间中，每个实例点通过特征向量来表示。比如用二维向量(39.9,5)来表示患者A体温39.9°，其它症状明显，或者四维向量(39.9，是，是，是)来表示患者B体温39.9°，咳嗽、乏力且打喷嚏。一般情况下，是需要把输入空间的数据转换到特征空间中，用特征向量来表示数据。书中提到了L_p距离，这里我们通过公式可以看到，实例点xi与实例点xj之间的L_P距离，实际上就是两个特征向量，各个分量差的绝对值P次方进行求和，再开P次根。

　　接下来看一下书中的距离度量。

　　可以从公式中直观的看出来，欧氏距离将各个分量差异平方之后求和，再开方，相当于把各个分量差异进行混合，杂糅在一起，将各个分量独立的差异，通过开根方整合到一起，偏向“和缓”的考虑两个特征向量整体的差异；曼哈顿距离则直接将各个分量的差异进行求和，各分量的差异“野蛮”的直接加在一起作为两个特征向量之间的距离；当P等于无穷大时，取各个分量差异的最大值，来表示两个特征向量之间的距离。该距离用分量差异最大值代表两特征向量距离的方法，提供给我们度量距离的一种思路：无论欧氏距离还是曼哈顿距离，各个分量的重要性是一样的，在现实场景中，不同的因素是具有不同重要性的。就是说，不同分量的差异，在特征向量距离度量的表示上，应该给不同的分量差异赋予不同的权重，这样得到的两个实例之间的距离更符合现实场景。例如体温过高和其它症状的表现，在衡量两个患者是否相似的距离上，体温高这个特征分量应该比其它症状更重要一些。

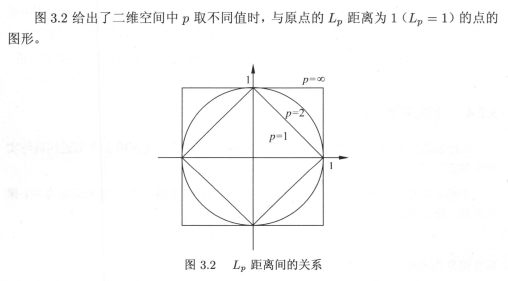
　　在图3.2中，可以看到p=1的菱形直线上，横轴到原点的距离加纵轴到原点的距离，始终为1；在p=2的圆形上，可以发现半径r=1，其实就是横轴纵轴勾股定理的斜边；在p=∞的正方形直线上，要取到横轴、纵轴差异的最大值，与原点距离为1就要选择最外的正方形。书中的例3.1说明了由不同的距离度量所确定的最近邻点是不同的。

2)K值的选择

　　K值的选择会对近邻法的结果产生重大影响，书中解释的很详细。表面上来说，K值的大小决定了多数表决时选取的最近邻个数，K值小，需要选取的邻居少，预测实例点仅与少数距离最近的实例点有关，这就会导致预测结果对近邻的实例点非常敏感，如果邻近的实例点恰巧是噪点，预测就会出错，导致过拟合。K=1时为最邻近法，只取最邻近的一个实例点进行判断，预测的结果只取决于一个相近实例点（所有鸡蛋都放在了一个篮子里），判断出错的几率非常大。

　　K值大，就相当于从更多的近邻实例点中进行多数表决，这就避免了所有鸡蛋放在同一个篮子里，减少了噪点对预测的影响，预测结果需要从多个实例中得出。但是，距离较远差距大的实例点也会对预测起作用，这会间接导致判断出错。K=N时，无论输入实例是什么，都将简单的预测它属于训练集中实例最多的类。

　　在实际应用中，K值的选择通常通过交叉验证法来选取最优的K值，一般是一个比较小的数值。

3)分类决策规则

　　K近邻法中的分类决策规则往往是多数表决，即由K个近邻的训练实例中的多数类决定输入实例的类别，也就是说最近邻10个患者中，需要输液的有7个人，3个人不需要输液，那么新的来诊人员判断为需要输液（取多数的类别）。书中对多数表决规则做了简单的数学解释，用来说明多数表决规则等价于经验风险最小化。

　　这里以0-1损失为例，通过第三个公式，我们可以看出，我们要想让误分类率减小，就要选择多数实例的类作为预测，在公式右端，若选择少数实例的类别，该值小，左端误分类率将增大。

K近邻法的实现：kd树

　　通过上述的学习，我们可以发现K近邻法主要考虑的问题，是如何在训练数据集中找到距离新实例点最近的K个邻近实例点，训练数据量越多，特征向量的维度越大，寻找最近的K个邻近点就越复杂。最简单的方法是进行线性扫描，这时要计算每个训练数据点与输入实例的距离，数据量大时，计算非常耗时。为了提高K近邻的搜索效率，可以考虑采用特殊的结构来存储训练数据，从而减少计算量，比如说kd树算法。

　　Kd树是一种对n维空间进行划分，并将分割超平面上的实例点进行存储，以便对其进行快速检索的二叉树。构造kd树相当于不断的用垂直于坐标轴的超平面将n维空间切分，构成一系列包含每个结点的n维超矩形区域。

　　Kd树的构造可以结合二叉搜索树的知识点去理解，既然结合二叉树的存储结构，那么就应该是采用二分的思想来方便查找过程。一维的情况下，二叉搜索树的思想是首先构造根节点，它是近邻法查找时的第一个实例点，应该具有一定的代表性，在数据的分布上，尽量居中，以根节点为中心分为左右两个子空间，递归进行构造。从二叉搜索树中，我们知道，整个二叉搜索树方便查找的关键是根节点的选取，也就是中间切分点的选择非常重要。

　　在kd树的构造中，同样是通过递归的方法，不断的选取合适的根节点，用超平面将n维空间划分为左右子空间，区别在于根节点的选取，根节点除了中位数的要求外，还要考虑不同维度的信息，本书中的算法，是将各个维度按顺序循环考虑，若有两个维度，在二叉树的第一层上，先用第一个维度上各个数值的中位点作为根节点划分为左右子空间；在递归的过程中，二叉树的第二层，是选取左右子树的根节点，这时的根节点是从第二个维度的各个数值中选取中位点；二叉树的第三层根节点，按维度顺序循环从第一个维度上选取子树数据集的中位点；二叉树的第四层根节点，按维度顺序循环再次从第二个维度上选取，接下来的各层根节点依此类推。

　　特征空间为二维时，是用直线将特征空间划分为矩形子区域，特征空间为三维及高维时，用超平面将特征空间划分为超矩形区域，递归进行划分，直到子区域内没有实例时终止。在算法3.2中，有两个地方可以改进：第一点，通过中位点选取切分点构造的kd树是平衡的，但搜索效率未必是最优的；第二点，按维度顺序循环选取切分点进行划分未必是最优的，可以依据不同维度上数据的分布规律来决定当前层选取切分点采用哪个维度?可深入。

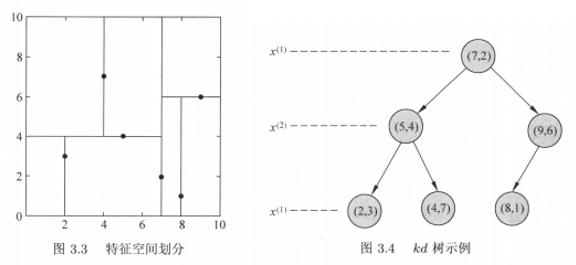
　　算法流程图：

　　书中以二维特征向量举例，也就是特征空间是一个二维平面，用直线将各个子空间划分开，划分的过程得到存储实例点的二叉树结构，二叉树的每层根节点，按照维度顺序循环作为切分点的选取来源。

搜索kd树

　　Kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量，以最近邻举例加以描述。给定一个目标点，搜索其最近的邻居，首先依次选取维度，按照二分查找的思想找到包含目标点的叶节点；然后从该叶节点出发，逆序退回父节点；在退回路径上，不断查找与目标点最邻近的节点，回退到根节点确定不可能存在更近的节点时终止。

　　在kd树搜索算法中，如果实例点是随机分布的，kd树搜索的平均计算复杂度为O(logN)，N是训练实例数，kd树适用于训练实例数远大于空间维数时的k近邻搜索，当特征向量维度大，也就是特征空间维数接近训练实例数时，效率迅速下降。

　　算法流程图：

　　示例：

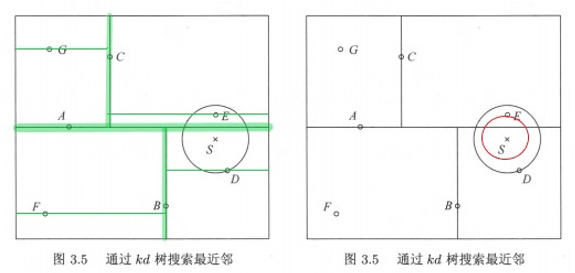
　　从示例图中可以看出，包含目标点的叶节点对应包含目标点的矩形区域，以此为叶节点的实例点作为当前最近点，目标点的最近邻一定在以目标点为中心并通过当前最近点的圆形内部。回退到当前节点的父节点，如果父节点的另一子节点的矩形区域与该圆形相交，那么需要在相交的区域内再次寻找与目标点更近的实例点，如果在相交区域内找到了更近的实例点，则将此点作为新的当前最近点；算法继续向更上一级父节点回退，继续上述过程，直到找到最近的实例点；如果父节点的另一节点的矩形区域与该圆形不相交，那该矩形区域内，肯定不存在更近的实例点；算法回退到根节点，直到不存在比当前最近点更近的实例点时，停止搜索。