Java实现二分图的最大权匹配

1 问题描述

何为二分图的最大权匹配问题？

最大权二分匹配问题就是给二分图的每条边一个权值，选择若干不相交的边，得到的总权值最大。

2 解决方案

解决这个问题可以用KM算法。理解KM算法需要首先理解“可行顶标”的概念。可行顶标是指关于二分图两边的每个点的一个值lx[i]或ly[j]，保证对于每条边w[i][j]都有lx[i]+ly[j]-w[i][j]>=0。如果所有满足lx[i]+ly[j]==w[i][j]的边组成的导出子图中存在一个完美匹配，那么这个完美匹配肯定就是原图中的最大权匹配。理由很简单：这个匹配的权值之和恰等于所有顶标的和，由于上面的那个不等式，另外的任何匹配方案的权值和都不会大于所有顶标的和。

但问题是，对于当前的顶标的导出子图并不一定存在完美匹配。这时，可以用某种方法对顶标进行调整。调整的方法是：根据最后一次不成功的寻找交错路的DFS，取所有i被访问到而j没被访问到的边(i,j)的lx[i]+ly[j]-w[i][j]的最小值d。将交错树中的所有左端点的顶标减小d，右端点的顶标增加d。经过这样的调整以后：原本在导出子图里面的边，两边的顶标都变了，不等式的等号仍然成立，仍然在导出子图里面；原本不在导出子图里面的边，它的左端点的顶标减小了，右端点的顶标没有变，而且由于d的定义，不等式仍然成立，所以他就可能进入了导出子图里。

初始时随便指定一个可行顶标，比如说lx[i]=max{w[i][j]|j是右边的点}，ly[i]=0。然后对每个顶点进行类似Hungary算法的find过程，如果某次find没有成功，则按照这次find访问到的点对可行顶标进行上述调整。这样就可以逐步找到完美匹配了。

值得注意的一点是，按照上述d的定义去求d的话需要O(N^{2)的时间，因为d需要被求O(N}2)次，这就成了算法的瓶颈。可以这样优化：设slack[j]表示右边的点j的所有不在导出子图的边对应的lx[i]+ly[j]-w[i][j]的最小值，在find过程中，若某条边不在导出子图中就用它对相应的slack值进行更新。然后求d只要用O(N)的时间找到slack中的最小值就可以了。

下面代码所使用的测试数据如下图：

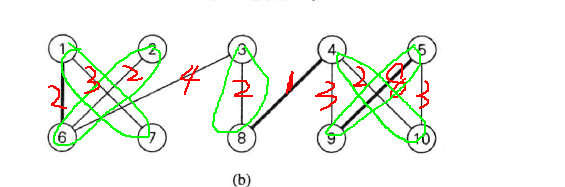
package com.liuzhen.practice;

import java.util.Scanner;

public class Main {
    public static int MAX = 100;
    public static int n;
    public static int[][] value = new int[MAX][MAX];   //给定二分图的权重值
    public static int[] lx = new int[MAX];   //记录二分图左半部分顶点的可行顶标
    public static int[] ly = new int[MAX];   //记录二分图右半部分顶点的可行顶标
    public static boolean[] sx = new boolean[MAX];//用于记录二分图左半部分顶点是否在最终结果中
    public static boolean[] sy = new boolean[MAX];//用于记录二分图右半部分顶点是否在最终结果中
    public static int[] pre = new int[MAX];  //用于记录最终结果中顶点y匹配的顶点x

    public boolean dfs(int x) {   //采用匈牙利算法找增广路径
        sx[x] = true;       //代表左半部分顶点x包含在最终结果中
        for(int y = 0;y < n;y++) {
            if(!sy[y] && lx[x] + ly[y] == value[x][y]) {
                sy[y] = true;   //代表右半部分顶点y包含在最终结果中
                if(pre[y] == -1 || dfs(pre[y])) {
                    pre[y] = x;
                    return true;
                }
            }
        }
        return false;
    }

    public int getKM(int judge) {
        if(judge == -1) {  //代表寻找二分图的最小权匹配
            for(int i = 0;i < n;i++)
                for(int j = 0;j < n;j++)
                    value[i][j] = -1 * value[i][j];  //把权值变为相反数，相当于找最大权匹配
        }
        //初始化lx[i]和ly[i]
        for(int i = 0;i < n;i++) {
            ly[i] = 0;
            lx[i] = Integer.MIN_VALUE;
            for(int j = 0;j < n;j++) {
                if(value[i][j] > lx[i])
                    lx[i] = value[i][j];
            }
        }

        for(int i = 0;i < n;i++)
            pre[i] = -1;      //初始化右半部分顶点y的匹配顶点为-1

        for(int x = 0;x < n;x++) { //从左半部分顶点开始，寻找二分图完美匹配的相等子图完美匹配
            while(true) {
                for(int i = 0;i < n;i++) {//每次寻找x的增广路径，初始化sx[i]和sy[i]均为被遍历
                    sx[i] = false;
                    sy[i] = false;
                }
                if(dfs(x))  //找到从x出发的增广路径，结束循环，寻找下一个x的增广路径
                    break;
                //下面对于没有找到顶点x的增广路径进行lx[i]和ly[i]值的调整
                int min = Integer.MAX_VALUE;
                for(int i = 0;i < n;i++) {
                    if(sx[i]) {  //当sx[i]已被遍历时
                        for(int j = 0;j < n;j++) {
                            if(!sy[j]) {  //当sy[j]未被遍历时
                                if(lx[i] + ly[j] - value[i][j] < min)
                                    min = lx[i] + ly[j] - value[i][j];
                            }
                        }
                    }
                }
                if(min == 0)
                    return -1;
                for(int i = 0;i < n;i++) {
                    if(sx[i])
                        lx[i] = lx[i] - min;
                    if(sy[i])
                        ly[i] = ly[i] + min;
                }
            }
        }

        int sum = 0;
        for(int y = 0;y < n;y++) {
            System.out.println("y顶点"+y+"和x顶点"+pre[y]+"匹配");
            if(pre[y] != -1)
                sum = sum + value[pre[y]][y];
        }
        if(judge == -1)
            sum = -1 * sum;
        return sum;
    }

    public static void main(String[] args) {
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        int k = in.nextInt();   //给定二分图的有向边数目
        for(int i = 0;i < k;i++) {
            int x = in.nextInt();
            int y = in.nextInt();
            int v = in.nextInt();
            value[x][y] = v;
        }
        System.out.println(test.getKM(1));
    }
}

运行结果：

10
0 2
1 3
0 2
0 4
2 2
2 1
3 3
4 2
3 8
4 3
y顶点0和x顶点2匹配
y顶点1和x顶点0匹配
y顶点2和x顶点1匹配
y顶点3和x顶点4匹配
y顶点4和x顶点3匹配