StanFord ML 笔记 第八部分

---

第八部分内容：

　　  1.正则化Regularization

　　2.在线学习(Online Learning)

　　3.ML 经验

---

1.正则化Regularization

　　

　　1.1通俗解释

　　　　引用知乎作者：刑无刀

　　　　解释之前，先说明这样做的目的：如果一个模型我们只打算对现有数据用一次就不再用了，那么正则化没必要了，因为我们没打算在将来他还有用，正则化的目的是为了让模型的生命更长久，把它扔到现实的数据海洋中活得好，活得久。

　　　　俗气的解释1：
　　　　　　让模型参数不要在优化的方向上纵欲过度。《红楼梦》里，贾瑞喜欢王熙凤得了相思病，病榻中得到一枚风月宝鉴，可以进入和心目中的女神XXOO，它脑子里的模型目标函数就是“最大化的爽”，所以他就反复去拟合这个目标，多次XXOO，于是人挂掉了，如果给他加一个正则化，让它爽，又要控制爽的频率，那么他可以爽得更久。

　　　　俗气的解释2：
　　　　　　假如马化腾心中的商业模型优化目标是让腾讯发展得更好，他的模型只有一个特征，就是张小龙，根据他的目标以及已有样本，它应该给张小龙赋予更大的权重，就可以一直让模型的表现朝这个目标前进，但是，突然有一天马化腾意识到：这样下去不行啊，他的权重大得没边的话，根本不可持续啊，他要是走了，他要是取代我了。于是马化腾就需要在优化这个目标的时候给这个唯一的特征加一个正则化参数，让权重不要过大，从而使得整个模型能够既朝着设定目标走，又不至于无法持续。

　　　　俗气的解释3：
　　　　　　我们这群技术男在公司里，如果模型目标是提高自身能力并最终能够在公司有一席之地，理想的优化方法是提高各种牛逼算法，各种高大上的计算平台的熟悉程度，尽量少开无谓的会议，少接领导扯淡的需求，但是如果只是这些的话，很可能在这个公司呆不太久，因为太关注自己的特征权重了，那么如果这个公司其实非常适合提升自己的能力，那么要能在这里呆久点，就得适当限制自己这些特征的权重绝对值，不要那么绝对坚持用到牛逼算法，偶尔也处理处理领导的扯淡需求，平衡一下，你的模型才能泛化得更广。

　　1.2用协方差解释

　　　　引用知乎作者：维吉特伯

　　　　其中 和 是列向量， 是矩阵，矩阵的每一行对应一个输入实例。把平方误差和（residual sum of squares, RSS）作为损失函数：　

　　　

　　　　假设要拟合一个线性的模型

　　　　写成矩阵形式就是

　　　　把 对 求偏导，并令偏导为0，

　　　　可以得出最小化损失的解：

　　　　然后再对损失添加正则化项（为了简化推导就用岭回归吧，添加 的平方项），下面我就直接写成向量形式啦：

　　　　同样，再对 求偏导，并令偏导为0

　　　　得出解为：

　　　　然后，对 进行奇异值分解（SVD）：

　　　　再拿训练得到的 再拟合一下训练数据，再套用一下奇异值分解：

　　　　对比一下没有正则化项的情况：

　　　　发现什么了吗，正则化之后， 和 之间相差了一个系数 。

　　　　因为 ，所以 。

　　　　这意味着加入正则化项的岭回归拟合的结果被缩小了 倍。那么，这个 的意义是什么呢？

　　　　再对输入作进一步假设来简化问题。如果输入 的均值为0，也就是对 进行预处理使得：

　　　　那么， 的协方差就可以通过 计算，并且根据之前的奇异值分解 ，有

　　　　这实际上也可以看作是 的特征分解。

　　　　所以 就是 的第 个特征值。

　　　   因此系数 可以看作根据协方差矩阵的特征值对不同成分进行收缩（个人理解为进行了一次隐式的特征选择），并且对特征值小的成分收缩更为剧烈（可以理解为通过把那些方差小的成分舍弃掉了，有点类似主成分分析，把那些重要的成分留下，次要的去除掉）。除了 之外， 也会影响收缩的程度。 值越大，收缩的越剧烈（需要更大的 来补偿 ），最终模型复杂度越低 。附上来自《The Elements of Statistical Learning》的图。

<span style="font-size: 14pt;"><img src="https://pic2.zhimg.com/50/v2-9408eada5159a960cf75bb3599089409_hd.png" data-rawwidth="689" data-rawheight="613" class="origin_image zh-lightbox-thumb" width="689" data-original="https://pic2.zhimg.com/v2-9408eada5159a960cf75bb3599089409_r.png"></span>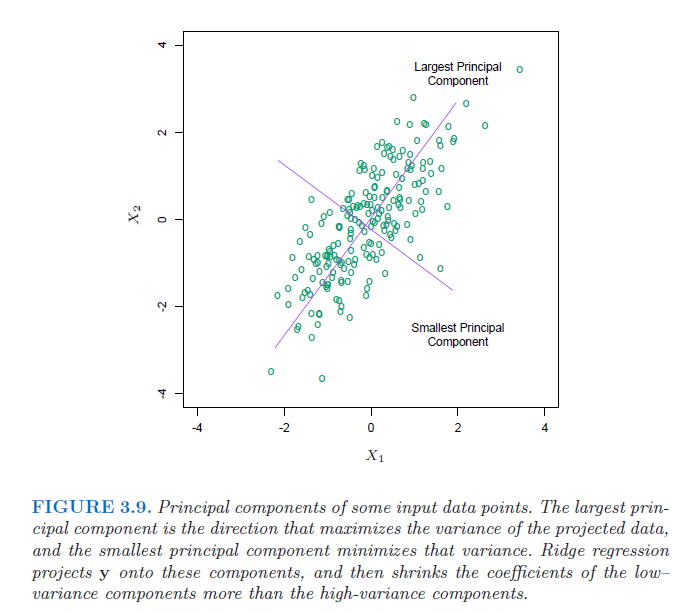

　　　　这样通过正则化项，就去减小了那些没用（次要）的特征带来的影响，防止过拟合。

　　

　　1.3Ng视频的讲解

　　　　http://blog.csdn.net/stdcoutzyx/article/details/18500441

　　　　

　　1.4个人总结

　　　　A.加入先验概率，正如我们都知道骰子每个概率是1/6，但是实验10次都是正面，我们能说正面概率为百分之百吗？加入前面的先验1/6效果就好多了。

　　　　B.在似然函数后面加上了aXX^T，后面的XX^T就是协方差，前面的a是比例，协方差的意思就是太离谱的数据权重就小，a的作用和高斯的均值一样。

　　

2.在线学习

　　批量学习：一次性给样本

　　 在线学习：多次性给样本

参考：https://www.zhihu.com/question/20700829(正则化的话题，很多知乎大神的回答)