Hdoj 1392.Surround the Trees 题解

Problem Description

There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him?

The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

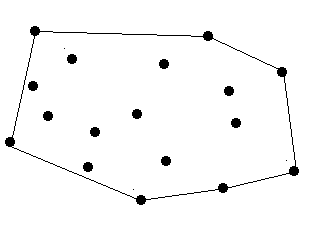
There are no more than 100 trees.

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.

Zero at line for number of trees terminates the input for your program.

Output

The minimal length of the rope. The precision should be 10^-2.

Sample Input

9
12 7
24 9
30 5
41 9
80 7
50 87
22 9
45 1
50 7
0

Sample Output

243.06

Source

Asia 1997, Shanghai (Mainland China)

---

思路

这就是找最小凸包并求其周长的过程，可以采用Graham算法，具体步骤如下：

• 读入一系列坐标并找到y坐标最小的坐标设置为\(p_0\)（如果x坐标相同就找x最小的）
• 对除了\(p_0\)以外的点按照逆时针以相对p0的极角排序，相同极角的点则保留一个离\(p_0\)最远的点
• 设置一个栈，前三个候选点先入栈，接下来让剩下的点一一入栈，去掉所有非左转的情况，由此，栈里的点就是凸包的点

具体看注释

代码

#include<bits/stdc++.h>
using namespace std;
struct point
{
	double x,y;
}a[110];

double dis(point a,point b)
{
	return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );
}

double crossMult(point a, point n1, point n2)
{
    return (n1.x-a.x)*(n2.y-a.y) - (n1.y-a.y)*(n2.x-a.x);
} //叉积，以a为基 

bool cmp(point n1, point n2)
{
	double k = crossMult(a[1],n1,n2); //叉积
	if( k>0 ) return true;  //叉积>0则说明a在b的顺时针方向上
	else
	{
		if( k==0 && dis(a[1],n1) < dis(a[1],n2) )  //叉积为0说明a和b在同一条直线上，且更远
			return true;
	}
	return false;
}

void sortByAngel(int n)
{
	point tmp;
	int k = 1;
	for(int i=2; i<=n; i++)
	{
		if( a[i].y < a[k].y || a[i].y == a[k].y && a[i].x < a[k].x)
			k = i;
	}  //找出p0
	tmp = a[1];
	a[1] = a[k];
	a[k] = tmp;
	sort(a+2, a+n+1,cmp);  //对除了p0以外的点逆时针以相对p0的极角进行排序
}

double Graham(int n)
{
	sortByAngel(n) ;
	point stack[110];
	double sum = 0.0;
	a[n+1] = a[1];
	stack[1] = a[1]; stack[2] = a[2]; stack[3] = a[3];
	int top = 3;//指向栈顶
	for(int i=4;i<=n+1;i++)   //这里是遍历到n+1，因为要回到最初的点
	{
		while( (crossMult(stack[top-1], stack[top], a[i])<=0) &&
		       top >= 3) top--; //保证是左转而且栈里面至少要有2个点（后面才能做叉积）
		top++;
		stack[top] = a[i];
	}
	for(int i=1;i<top;i++)//这里i<top即可，因为后面要访问的是stack[i],stack[i+1]
	{
		sum += dis(stack[i],stack[i+1]);
	}
	return sum;
}

int main()
{
	int n;
	while(cin>>n)
	{
		if(0==n) break;
		for(int i=1;i<=n;i++)
			cin >> a[i].x >> a[i].y;

		if(1==n)
			cout << "0.00" << endl;
		else if(2==n)
			printf("%.2lf\n",dis(a[1],a[2]));
		else
		{
			double ans = Graham(n);
			printf("%.2lf\n",ans);
		}
	}
	return 0;
}