[luogu3620][APIO/CTSC 2007]数据备份【贪心+堆+链表】

题目描述

你在一家 IT 公司为大型写字楼或办公楼(offices)的计算机数据做备份。然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。
已知办公楼都位于同一条街上。你决定给这些办公楼配对(两个一组)。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。
然而，网络电缆的费用很高。当地电信公司仅能为你提供 K 条网络电缆，这意味着你仅能为 K 对办公楼(或总计 2K 个办公楼)安排备份。任一个办公楼都属于唯一的配对组(换句话说，这 2K 个办公楼一定是相异的)。
此外，电信公司需按网络电缆的长度(公里数)收费。因而，你需要选择这 K对办公楼使得电缆的总长度尽可能短。换句话说，你需要选择这 K 对办公楼，使得每一对办公楼之间的距离之和(总距离)尽可能小。
下面给出一个示例，假定你有 5 个客户，其办公楼都在一条街上，如下图所示。这 5 个办公楼分别位于距离大街起点 1km, 3km, 4km, 6km 和 12km 处。电信公司仅为你提供 K=2 条电缆。

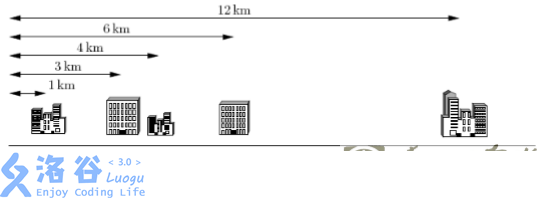
上例中最好的配对方案是将第 1 个和第 2 个办公楼相连，第 3 个和第 4 个办公楼相连。这样可按要求使用 K=2 条电缆。第 1 条电缆的长度是 3km―1km = 2km，第 2 条电缆的长度是 6km―4km = 2 km。这种配对方案需要总长 4km 的网络电缆，满足距离之和最小的要求。

分析

题目大意
给你n个数，两个数分成一组，一共分成k组，使得相差的和最小。
显然，一组的数一定是相邻的，那么考虑最简单最不对的暴力就是找出所有的差然后排序取前k个。
明显不对，那么我们就先差分求出两个数之间的差，然后全部放到一个优先队列中，因为我们只能有k个。（慕容宝宝大佬好巨啊），慕容宝宝大佬说什么反悔机制？？？简单的说就是因为不能取相邻的，那么相邻3个的差分都不能拿，那么我们就将这三个打一个包。表示的是一开始贪心时我们选择的是中间这一个。
之后再优先队列查询到这个不需要的时候，我们就将这个，换掉，也就是\(a[left]+a[right]-a[mid]\)，也就是将两边的加回来，将这个点删除。
删除操作问题，我们可以用双向链表来维护就可以了。

ac代码

#include <bits/stdc++.h>
#define ll long long
#define ms(a, b) memset(a, b, sizeof(a))
#define inf 0x3f3f3f3f
#define N 100005
using namespace std;
template <typename T>
inline void read(T &x) {
    x = 0; T fl = 1;
    char ch = 0;
    while (ch < '0' || ch > '9') {
        if (ch == '-') fl = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= fl;
};
struct node {
    int id, val;
    node(int id, int val): id(id), val(val){}
    bool operator <(const node &rhs) const {
        return val > rhs.val;
    }
};
int f[N], a[N], nxt[N], lst[N];
int n, k;
priority_queue<node>q;
ll ans = 0;
int main() {
    read(n); read(k);
    for (int i = 1; i <= n; i ++) {
        read(a[i]);
    }
    for (int i = 1; i < n; i ++) {
        f[i] = a[i + 1] - a[i];
        nxt[i] = i + 1;
        lst[i] = i - 1;
    }
    nxt[n - 1] = 0;
    for (int i = 1; i < n; i ++) q.push(node(i, f[i]));
    for (int i = 1; i <= k; i ++) {
        node nw = q.top();
        q.pop();
        if (nw.val != f[nw.id]) {
            ++ k;
            continue;
        }
        ans += nw.val;
        int left = lst[nw.id], right = nxt[nw.id];
        nxt[nw.id] = nxt[right];
        lst[nxt[nw.id]] = nw.id;
        lst[nw.id] = lst[left];
        nxt[lst[nw.id]] = nw.id;
        f[nw.id] = (left && right) ? min(inf, f[left] + f[right] - f[nw.id]): inf;
        f[left] = f[right] = inf;
        q.push(node(nw.id, f[nw.id]));
    }
    printf("%lld\n", ans);
    return 0;
}