MT【248】$f(x)=\dfrac{1}{x-1}+\dfrac{1}{x-b}$的性质

探讨函数$f(x)=\dfrac{1}{x-a}+\dfrac{1}{x-b}$其中$a<b$的几个性质

分析:
对称性:关于$(\dfrac{a+b}{2},0)$证明提示:$f(x)+f(a+b-x)=0$且定义域关于$(\dfrac{a+b}{2},0)$对称
单调性:单调递减区间$(-\infty,a),(a,b),(b,+\infty)$,证明提示:用单调性的定义
渐进性:$\lim\limits_{x\rightarrow-\infty}f(x)=0$;$\lim\limits_{x\rightarrow+\infty}f(x)=0$;
$\lim\limits_{x\rightarrow a^+}f(x)=+\infty$;$\lim\limits_{x\rightarrow a^-}f(x)=-\infty$
$\lim\limits_{x\rightarrow b^+}f(x)=+\infty$;$\lim\limits_{x\rightarrow b^-}f(x)=-\infty$
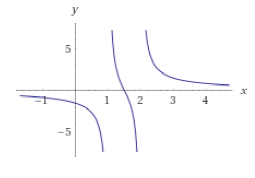
最后提供一张$a=1,b=2$时的图.