选择排序--java进阶day06
1.选择排序
https://kdocs.cn/l/ciMkwngvaWfz?linkname=150996881

了解了选择排序之后,我们来找其中的规律
2.规律
选择排序就是一个元素和数组后续元素依次进行比较,那么我们先观察主动去比较的那个元素
发现,该元素的索引在不断地加1,想要达成这种效果我们直接遍历数组,i就是这样变化的
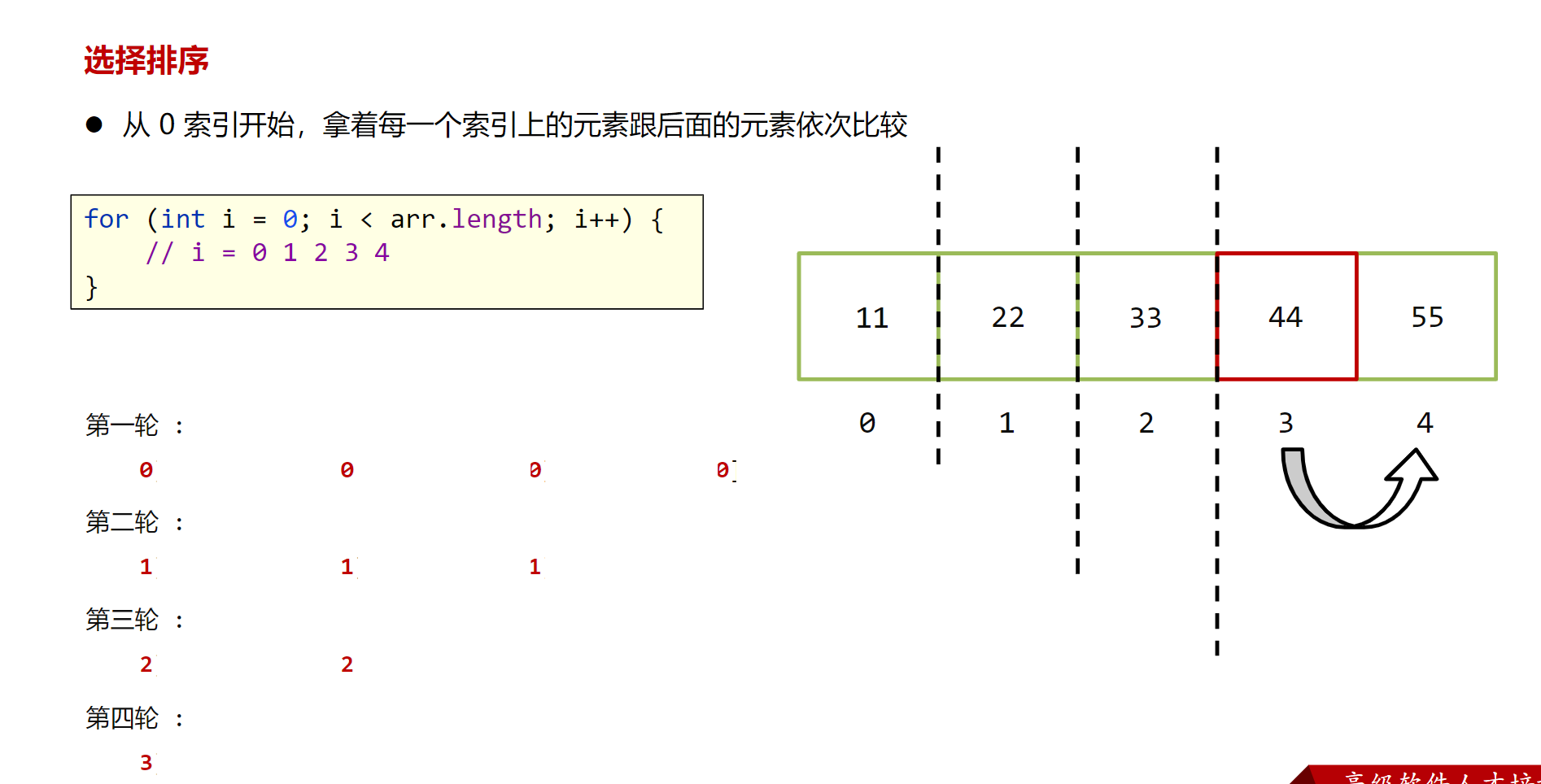
不过上图中,i多出了一个4,我们让循环条件减1即可

后续的元素我们就要再遍历一次数组来获取

接下来再看这些剩余数据的索引

重点看第一列
当i是0时,j就为1,i是1时,j就为2,i是3时,j就为4

很明显,j是i+1
所以,这些元素的比较实际上就是arr[i]和arr[j]的比较

.
实际代码
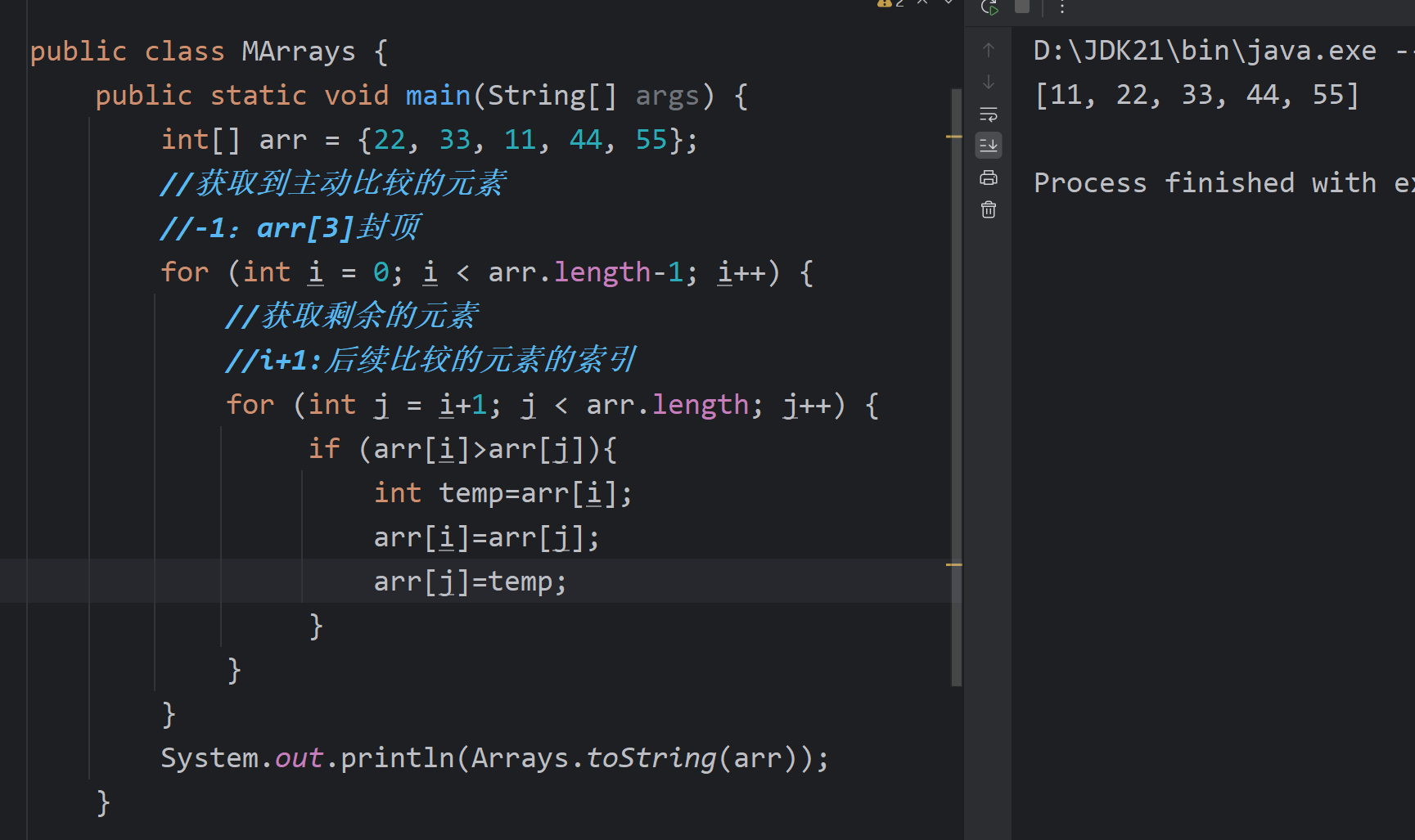
选择排序--java进阶day06的更多相关文章
- 基本排序算法——选择排序java实现
选择排序与冒泡排序有很大的相同点,都是一次遍历结束后能确定一个元素的最终位置,其主要思路是,一次遍历选取最小的元素与第一个元素交换,从而使得一个个元素有序,而后选择第二小的元素与第二个元素交换,知道, ...
- 选择排序-java
排序-选择排序 基本思想:在待排序子表中找出最大(小)元素, 并将该元素放在子表的最前(后)面. 平均时间:O(n2) 最好情况:O(n2) 最坏情况:O(n2) 辅助空间:O(1) 稳定性:不稳定 ...
- 直接选择排序----java实现
直接选择排序思路: 从待排序数据中选择第一个假定为最小的下标,然后他后面的与他循环比较,得到真的最小值下标,然后最小值前的那一区段依次后移,并把最小值赋值给第一个元素.第二次时,假定第二个为最小,然后 ...
- 选择排序Java版
package dataStructureAlgorithmReview.day01; import java.util.Arrays; /** * * @author shundong * */ p ...
- 选择排序java代码
/** * 选择排序 * * 原理:将最小值与数组第1个即array[0]交换,第二次则忽略array[0],直接从array[1]至array[array.length-1]中 * 选择出最小值与a ...
- 选择排序java
先简述选择排序,然后上代码 进行选择排序就是将所有的元素扫描一遍,从中挑选(或者说是选择,这正是这个排序名字的由来)最小的一个元素,将这个最小的元素与最左边的元素交换位置 ,现在最左边的元素就是有序的 ...
- 冒泡排序与简单选择排序——Java实现
1.冒泡排序 1)原理说明:反复遍历要排序的数列,一次比較两个元素,假设他们的顺序错误就把他们交换过来.走訪数列的工作是反复地进行直到没有再须要交换,也就是说该数列已经排序完毕. 2)代码实现: pa ...
- 冒泡排序和选择排序-java
冒泡排序 假设有一数组int [] arr = {9,5,4,10,2};原理是第一个元素和第二个比较,如果前者大于后者便交换位置,然后第二个元素和第三个元素比较,如果前者大于后者便交换位置.以此类 ...
- 排序算法入门之选择排序-Java实现
本文参考http://blog.csdn.net/m0_37568091/article/details/78023705 选择排序是先从对象数组中选出最小的放在第一个位置,再从剩下的元素中选择次小的 ...
- 选择排序java实现
package text.algorithm; /** * 选择排序 * O(n^2);空间复杂度O(1); */public class SelectionSort { public static ...
随机推荐
- PostGIS代码操作简介
PostGIS代码操作简介 1. 代码操作POSTGIS的可选方案 jdbc postgis-java geotools gdal 2. JDBC public void testJdbc() { S ...
- 记录使用socket.io的使用
今天记录一下node.js的egg框架搭建的socket.io,前端联合使用 首先得引入socket.io的js,我这边是用的下载到本地的一个js 引入:const io = require('../ ...
- Linux 压缩命令集合
01. tar格式 解包:tar xvf FileName.tar 打包:tar cvf FileName.tar DirName(注:tar是打包,不是压缩!) 02. gz格式 解压1:gunzi ...
- Java验证邮箱是否有用的实现与解析
在现代互联网应用中,邮箱验证是一个常见的需求.通过邮箱验证,开发者可以确保用户提供的邮箱地址是有效的,从而在后续的操作中,如密码重置.通知发送等,依赖这些有效的邮箱地址.本文将详细介绍如何使用Java ...
- java多线程---总结(2)
ThreadPoolExecutor 官方API解释线程池的好处: (1)通过重用线程池中的线程,来减少每个线程创建和销毁的性能开销. (2)对线程进行一些维护和管理,比如定时开始,周期执行,并发数控 ...
- uni-app组件 信息列表组件
之前我一直在,要想提高自己的代码质量, 就一定要封装自己的组件, 所以我就尽量使用自己的组件.这样可以提高自己的效率 写组件的好处:减少代码的冗余 封装组件的时候,为了不让子元素的padding, 影 ...
- @所有Mac用户 刺客信条系列登陆Mac平台!
[历史性的跨越] 在无数Mac游戏爱好者的热切期盼中,终于将风靡全球的3A级巨作--刺客信条系列,成功移植至MacOS系统!这意味着,无论是穿梭于中世纪欧洲的隐秘巷弄,还是翱翔于维多利亚时代的伦敦天际 ...
- ORACLE SELECT INTO 赋值为空,抛出 NO DATA FOUND 异常
例子: DECLARE ORDER_NUM VARCHAR2(20); BEGIN SELECT S.ORDER_NUM INTO ORDER_NUM FROM SALES_ORDER S WHERE ...
- Arduino 语法--数组
数组是一种可访问的变量的集合.Arduino的数组是基于C语言的,实现起来虽然有些复杂,但使用却很简单. 一.创建或声明一个数组 数组的声明和创建与变量一致,下面是一些创建数组的例子. arrayIn ...
- axios 发送 form-data 请求和 x-www-form-urlencoded请求以及相关问题
问题 not supported { "msg": "Content type 'multipart/form-data;boundary=--------------- ...
