UNR 6. D2T2 神隐

\(\mathbf{Part. -1}\)

这是一道交互题。

hehe 蚤决定花费几天时间，游览下山市的最著名的旅游景点 —— 吓山。

吓山，以高低纵横，崔巍秀丽，错综复杂的地形闻名。据说无论用什么地图导航，都不能保障你在山中不迷路。

之所以会出现这样的情况，是因为吓山中的路，在没有光的时候都会发生 “神隐”。在“神隐”状态下，人们无法察觉到这条路的存在，很容易就迷路了。

吓山的地图可以简化为一个 \(n\) 个节点，编号为 \(0 \sim n-1\) 的树。它有 \(n - 1\) 条边，其中第 \(i\) 条边为 \((u_i, v_i)\)（\(0 \leq i \lt n - 1\)）。每条路上都装有路灯。

为了攻略吓山，hehe 蚤和它的小伙伴们试图绘制吓山的地图。

1. hehe 蚤事先从吓山管理员那里拿到了吓山每条路的路灯的控制权。hehe 蚤会进行若干次询问，每次询问时 hehe 蚤都会打开一部分路的路灯，并关闭剩下的路灯。当一条路上的路灯打开时，这条路就真实存在；当路灯关闭时，这条路就会 “神隐”，等效于不存在。
2. 对于每个询问，hehe 蚤的小伙伴们都会进行一番实地考察，告诉 hehe 蚤吓山在当前状态下的哪些节点是可以通过道路相互连通的。
3. 最后 hehe 蚤会根据询问结果总结出一份地图，即恢复出这棵树的形态。

为了更高效地解决问题，hehe 蚤将其抽象为了一道交互题。有一棵未知的树，你需要对交互库进行若干次询问，来恢复这棵树的形态。每次询问时，你需要给出一个长度为 \(n - 1\) 的 \(01\) 向量 \(A\)，然后交互库会将每条满足 \(A_i = 1\) 的边 \((u_i, v_i)\) 加入一张新的空图 \(G\) 中，并返回其中每一个连通块（再删除这个图）。最后，你需要输出这棵树的所有边（顺序、方向任意）。

\(\mathbf{Part. 1}\)

我们定义 \(e_x\) 表示第 \(x\) 条边。我们说 \(e_x\) 连接的两个连通块分别为 \(S_x, T_x\)（如下图）。

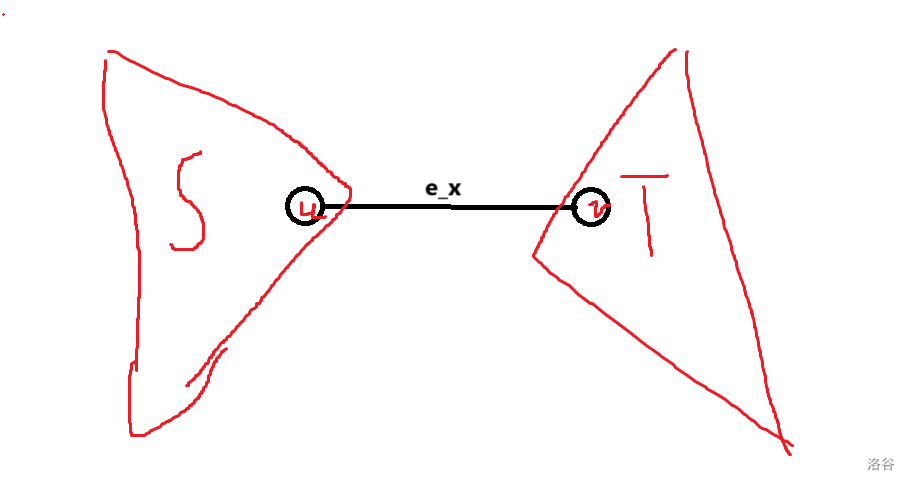
我们考虑观察每条边需要的询问信息。如果说对于一个询问，第 \(x\) 条边存在，则 \(u\) 和 \(v\) 在同一连通块内；第 \(x\) 条边不存在，则 \(u\) 和 \(v\) 不属于同一连通块内。考虑哪一种情况信息更多。

• 对于第 \(x\) 条边存在的所有询问，假设询问集为 \(Q\)。对于这些询问，我们只知道 \(x\) 在分别每个询问中不可能连接哪些点。我们可以尝试保证在这些询问中，除 \(e_x\) 外每条边都至少不存在一次¹。显然，只有 \((u, v)\) 这一个点对对于所有询问，\(u, v\) 都一直在同一连通块中。
• 对于第 \(x\) 条边不存在的所有询问，假设询问集为 \(Q\)。对于这些询问，我们只知道 \(x\) 在分别每个询问中可能连接哪些点。我们可以尝试保证在这些询问中，除 \(e_x\) 外每条边都至少存在一次。对于 \(a\in S_x, b\in T_x\)，都有 \((a,b)\) 点对，对于所有相关询问，\(u, v\) 不属于同一连通块（但是 \((a,b)\) 不一定是一条边，它可以是一条路径）。

综上，列出上述两种情况的结论：

• 只有 \((u, v)\) 这一个点对，对于所有 \(x\) 边存在的询问，\(u, v\) 一直在同一连通块中，此时第 \(x\) 条边连接 \(u, v\)。
• 对于 \(a\in S_x, b\in T_x\)，对于所有 \(x\) 边消失的询问，\((a, b)\) 不在同一连通块。此时，我们无法区分 \((a, b)\) 和真正的 \(u, v\)。

显然，第一种会更强。于是考虑分析第一种情况。

PS：实际上，第二种情况也可以做出这道题。

由 1 处，我们需要对于所有边 \(x\)，在 \(x\) 存在的询问中，边 \(y\) 至少消失一次。因此，我们要考虑构造每个边 \(x\) 存在的询问集合 \(Q_x\)，使得对于任意 \(i\neq j\)，都有 \(Q_{i} \not\subseteq Q_j\)。（因为如果 \(Q_j \subseteq Q_i\)，则 \(e_i\) 要么在 \(Q_j\) 中全部出现，要么在 \(Q_i\) 中存在询问没有出现）

这是一个经典问题，\(\binom{\text{limit}}{\frac{\text{limit}}{2}}\) 为最大值。具体见 CF1365G Secure Password 的 \(\mathbf{Part. 2}\)。复杂度瓶颈在于计算每条边是否一直在同一连通块，\(\mathcal{O}(n^2 \times \text{limit})\)。

\(\mathbf{Part. 2}\)

我们发现，如果想要去直接优化复杂度瓶颈，那将会非常困难，因为每一个可能的点对 \((u, v)\) 我们都要判断它可不可能是真的边。光是点对数量就有 \(\mathcal{O}(n^2)\) 个。

那优化方法显而易见：我们能不能对于点对分组，每次判断一个组内的点对，来减少计算量？这要求对于一个组内的点对可以一起判断，而且不能说存在 \(100\) 条边合法之类的事情发生。最好的话，我们要让同一组内合法的点对尽量少，比如说只有一个？

考虑按照点来对点对进行分组。对于第 \(x\) 个点，我们要一起判断对于所有 \(i \neq x\)，\((x, i)\) 这个点对是否是真的边。显然，对于第 \(x\) 个点，存在 \(deg_x\) 个点对合法，而这个 \(deg_x\) 可能很大，比如菊花图。当然，\(deg_x\) 一定存在点非常小，树的叶子就一定是 \(1\)。

显然，一上来不可能去考虑 \(deg_x\) 很大的情况。通过化繁为简的思想，我们先从简单的情况入手，考虑寻找哪些分组只有一个合法点对。

假设我们当前在考虑 \(x\)。那么，如果它只有一个合法点对，说明 \(x\) 为叶子节点，而连接这个叶子节点的边则是合法点对。显然，当这条边存在时，考虑观察 \(x\) 所在的连通块大小，显然，肯定一直 \(> 1\)。但是当这条边不存在时，\(x\) 所在连通块大小永远为 \(1\)，而这是非叶子节点做不到的（这时候，性质对象从边变成了点，所以计算量减少一个量级）。

因此，考虑维护每个点在所有询问中的连通块大小的情况。显然，在判断完最简单的叶子后，我们类似于 topo 排序把叶子删除，同时更新相邻点的连通块大小信息。一直剥叶子，化繁为简，即可通过这道题目。复杂度为 \(\mathcal{O}(n\times \text{limit}) = \mathcal{O}(n \log n)\)。

\(\mathbf{Part. +\infin}\)

这一部分是更新部分。

其实上面的方法是有漏洞的，我们不知道每个点的父亲节点！这样我们完全不能输出这颗树，而且这个还不是很好求。但是由于前面剥叶子的做法我们只需要删掉这个点，对于每个询问更新信息，是不需要知道每个点的父亲节点的，所以原树的拓扑序我们还是能求出来的。

那我们现在有什么信息？我们知道每个点所在的连通块信息，且知道每个点的拓扑序。

假设当前我们在计算第 \(x\) 个节点的父亲节点。\(x\) 所在的所有连通块中，深度最低的点（也是所有点的 LCA）显然是 \(x\) 的祖先。 而由于 1，在 \((x, fa_x)\) 这条边存在时，\((fa_x, fa_{fa_x})\) 肯定消失过至少一次。所以，肯定有一个 \(x\) 所属的连通块，这个连通块的 LCA 是 \(fa_x\)。因此，考虑对于所有连通块，寻找除了 LCA 为 \(x\) 的其他 LCA 深度最大的那个点。

但是我们不知道深度。怎么办呢？由于 \(x\) 所在的所有连通块，LCA 都是 \(x\) 的祖先，又由于有祖先关系的两个点，他们的深度关系可以通过拓扑序来判断，所以我们把深度改成拓扑序即可，寻找除了 LCA 为 \(x\) 的其他 LCA 拓扑序最小值，其中 LCA 是连通块中拓扑序的最大值。