使用Python可视化洛伦兹变换

引言

大家好！今天我们将探讨一个非常有趣且重要的物理概念—洛伦兹变换。它是相对论的核心内容之一，描述了在高速运动下，时间、长度以及其他物理量是如何发生变化的。通过使用 Python 进行可视化，我们不仅可以更好地理解这个概念，还能感受到物理世界中的奇妙之处。

什么是洛伦兹变换？

洛伦兹变换是描述不同惯性参考系之间物理量转换的数学关系。在经典力学中，我们通常认为时间和空间是绝对的，但在爱因斯坦的特殊相对论中，时间和空间都是相对的，它们依赖于观察者的运动状态。

洛伦兹变换主要涉及两个物理量：

• 时间膨胀：当一个物体以接近光速的速度运动时，观察者看到的物体的时间会变慢。
• 长度收缩：当一个物体以接近光速的速度运动时，观察者看到物体的长度会变短。

这些现象虽然在日常生活中不易察觉，但在高速运动的情况下(比如粒子加速器中的粒子运动)，却是显而易见的。

洛伦兹变换的基本公式如下：

时间变换：\(t{\prime} = \gamma \left( t - \frac{v x}{c^2} \right)\)

空间变换：\(x{\prime} = \gamma (x - v t)\)

其中：

• t 和 x 是在静止参考系下的时间和位置。
• \(t{\prime}\) 和 \(x{\prime}\) 是在运动参考系下的时间和位置。
• v 是相对速度。
• c 是光速，约为 \(3 \times 10^8 \, \text{m/s}\) 。
• \(\gamma\) 是洛伦兹因子，定义为：\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\)

为什么要可视化洛伦兹变换？

洛伦兹变换的公式看起来可能有些抽象，难以理解。通过 Python 的可视化，我们能够直观地看到在不同速度下，时间膨胀和长度收缩是如何发生的。通过改变物体的速度，我们可以观察到这些效应如何随着速度的增大而显著变化。

用 Python 进行洛伦兹变换可视化

我们可以通过 Python 来绘制洛伦兹变换的图像，帮助大家更好地理解时间膨胀和长度收缩。以下是一个简单的实现。

安装所需库

首先，我们需要安装 matplotlib 库，用于绘制图形：

pip install matplotlib

编写代码实现可视化

# coding=utf-8
import matplotlib

matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt

# 常量
c = 3e8  # 光速 (m/s)

# 洛伦兹因子计算函数
def lorentz_factor(v):
    return 1 / np.sqrt(1 - (v ** 2 / c ** 2))

# 时间膨胀计算函数
def time_dilation(t, v):
    gamma = lorentz_factor(v)
    return gamma * t

# 长度收缩计算函数
def length_contraction(x, v):
    gamma = lorentz_factor(v)
    return x / gamma

# 速度范围
velocities = np.linspace(0, 0.9 * c, 100)

# 设置静止的时间和长度
t_0 = 1  # 静止下的时间（单位：秒）
x_0 = 10  # 静止下的长度（单位：米）

# 计算不同速度下的时间膨胀和长度收缩
time_dilated = time_dilation(t_0, velocities)
length_contracted = length_contraction(x_0, velocities)

# 绘制图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))

# 时间膨胀图
ax1.plot(velocities / c, time_dilated, label="Time Dilation")
ax1.set_xlabel("Speed(v/c)")
ax1.set_ylabel("Dilated Time(t')")
ax1.set_title("Time Dilation")
ax1.grid(True)

# 长度收缩图
ax2.plot(velocities / c, length_contracted, label="Length Contraction", color='red')
ax2.set_xlabel("Speed(v/c)")
ax2.set_ylabel("Contracted Length(x')")
ax2.set_title("Length Contraction")
ax2.grid(True)

# 保存图形
plt.tight_layout()
plt.savefig('Lorentz.png')

代码解析

• 洛伦兹因子计算：lorentz_factor(v)函数计算了洛伦兹因子 \(\gamma\)，它与物体的速度 v 密切相关。随着速度接近光速，\(\gamma\) 会变得越来越大，从而导致时间膨胀和长度收缩。

• 时间膨胀和长度收缩计算：分别通过 time_dilation(t, v)和 length_contraction(x, v)函数，计算了在不同速度下，时间膨胀和长度收缩的情况。

• 绘制图形：我们绘制了两个图，一个表示时间膨胀，另一个表示长度收缩。横坐标表示速度 v 相对于光速 c 的比值，而纵坐标分别表示膨胀后的时间和收缩后的长度。

结果展示

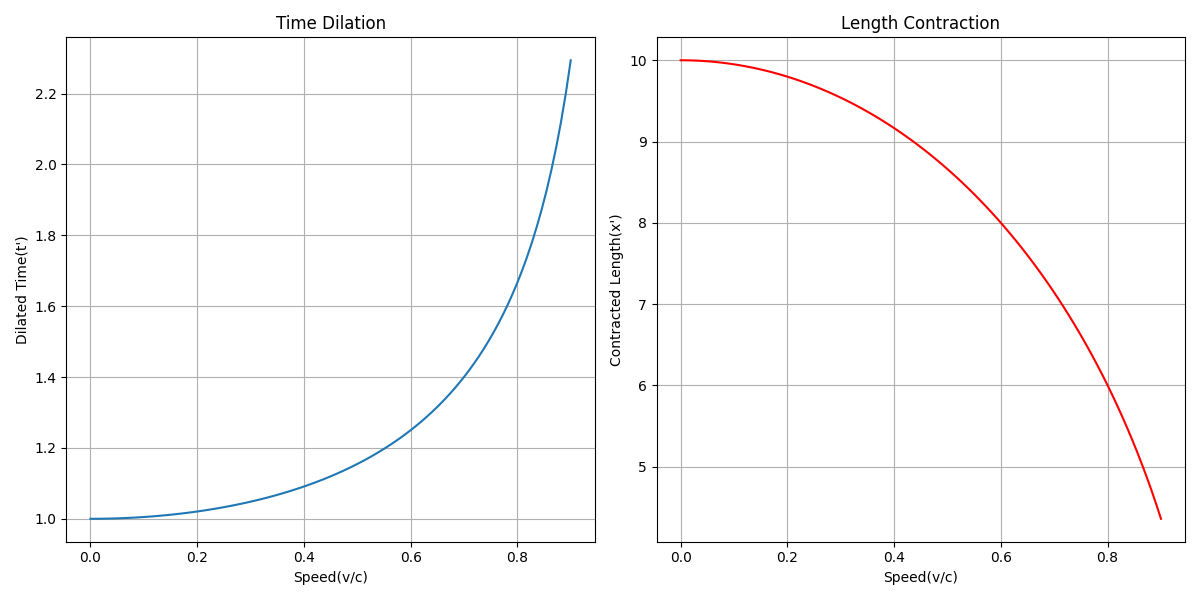
运行代码后，我们可以得到两幅图：

时间膨胀：随着速度的增加，时间膨胀变得越来越显著。当物体的速度接近光速时，时间几乎停止流动。这意味着在高速运动的物体上，时间会变得非常慢。

长度收缩：随着速度的增加，物体的长度在运动方向上会变得越来越短。当物体的速度接近光速时，它的长度几乎会完全收缩。

总结

通过今天的文章，我们用 Python 成功地可视化了洛伦兹变换，并直观地展示了时间膨胀和长度收缩的效果。随着物体速度的增大，时间和空间的变化变得尤为显著，尤其是在接近光速时，物理世界呈现出与我们常规经验截然不同的特性。

洛伦兹变换不仅仅是一个数学公式，它揭示了相对论中非常重要的物理现象。通过这种可视化的方式，我们可以更清楚地理解这些现象，感受到相对论的魅力。如果你对相对论和洛伦兹变换感兴趣，可以深入探索更复杂的物理模型和实验现象。

希望这篇文章能够激发你对相对论和物理学其他领域的兴趣！欢迎在评论区分享你的想法和问题！