层次分析法的Python实现--数学建模学习日志

数学建模比赛即将到来，大家应该都投身于学习当中了，b站上比较热门的一个课程是

b站数学建模学习视频

在这里讲解了数学建模常见的方法和写论文的要点，同时up主贴心地有所有方法的源码实现，但是全部都是matlab的代码。作为计算机人，python对我肯定是要比matlab熟悉的，所以我自己在学习过程中研究了如何用python实现这些方法，在这里分享给各位！

一、层次分析法

层次分析法（Analytic Hierarchy Process）是一种由美国运筹学家托马斯·萨蒂（Thomas L. Saaty）于20世纪70年代提出的多准则决策方法。它将复杂问题分解为层次结构，通过定量与定性结合的方式，对备选方案进行优先排序。核心思想是通过构建判断矩阵，量化决策者的主观判断，最终计算各元素的权重。

主要分为以下几个步骤：（图片内容来自up主的 ppt）



  当然，讲解这个方法不是我这篇文章的重点，详细方法请到视频中观看，下面介绍如何使用python实现层次分析方法。

二、Python实现层次分析法

1.导入相关库

层次分析法主要对矩阵进行操作，所以主要使用的是numpy库，各位如果想详细了解numpy库的各种操作，可以见我的这篇博客：

[numpy学习笔记]（https://blog.csdn.net/2401_83372039/article/details/146212725?spm=1001.2014.3001.5501）

接下来主要就是代码的实现展示，我就不一一讲解numpy的操作了，大家可以照着我上面的博客来查用法，当作字典用即可。所有涉及用法上面均有！！！

import numpy as np

2.读取矩阵

A.size返回的是矩阵的尺寸是长乘宽的结果，shape是返回以元组形式储存的长和宽。层次分析法的矩阵都是方阵，所以随便保存一个即可。

输入矩阵：

[[1,2,5],[1/2,1,2],[1/5,1/2,1]]

A=np.array(eval(input("请输入矩阵A=")))
print(A)
n=A.size    #这里的size结果是3*3=9
n=A.shape[0]  #这里才是获取了行数

[[1. 2. 5. ]

[0.5 1. 2. ]

[0.2 0.5 1. ]]

3.算数平均法求权重

#按照列求总值
A_sum=np.sum(A,axis=0)
stand_A=A/A_sum
print(stand_A)
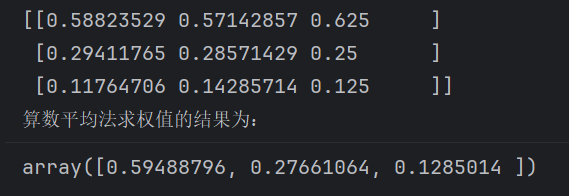
print("算数平均法求权值的结果为：")
w1=np.sum(stand_A,axis=1)/n
print(w1)

4.特征值法求权重

A_elg=np.linalg.eig(A)
print(A_elg)  #eigenvalues是特征值，eigenvectors是特征向量
max_elg=np.max(A_elg[0]).real
print(max_elg)
#获取最大特征值处的特征向量
w2=A_elg[1][:,A_elg[0]==max_elg]
print("特征值法求权值的结果为：")
#归一化
print(w2/np.sum(w2.real))
#我们可以将两种方法平均
w3=(w1+w2)/2
w3

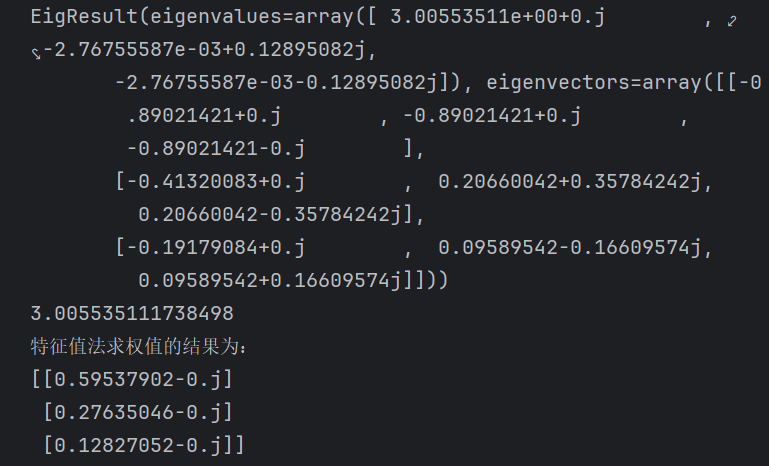
层次分析法中，我们可以将两种方法结合起来，求个均值来作为我们的权重，当然要是不结合，更推荐使用特征值法求权重。

特征值和特征向量的计算会带上虚数，这里使用A.real来只是用实数部分。

注意， np.linalg.eig()函数会返回两个值，第一个是特征值第二个是特征向量，和matlab的相反。

5.计算一致性比例CR

• 注意：第一步就应该要检验矩阵是否符合一致性，写此处只是为了编程方便！！！

CI=(max_elg-n)/(n-1)
RI=np.array( [0.00, 0.00, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.51, 1.54, 1.56, 1.58, 1.59])  #注意RI最大支持RI是n=15！！！
CR=CI/RI[n-1]
if CR<0.1:
    print("一致性检验通过")
    print(CR)
else:
    print("一致性检验未通过")
    print("请重新输入数据")

一致性检验通过

0.0047716480504293775

当然，RI是查表得到的，这个数据根据文献不同数值上可能有微小差距，影响不会太大。