Day7 备战CCF-CSP练习

Day 7

题目描述

栋栋最近开了一家餐饮连锁店，提供外卖服务。

随着连锁店越来越多，怎么合理的给客户送餐成为了一个急需解决的问题。

栋栋的连锁店所在的区域可以看成是一个 \(n×n\)的方格图（如下图所示），方格的格点上的位置上可能包含栋栋的分店（绿色标注）或者客户（蓝色标注），有一些格点是不能经过的（红色标注）。

方格图中的线表示可以行走的道路，相邻两个格点的距离为 \(1\)。

栋栋要送餐必须走可以行走的道路，而且不能经过红色标注的点。

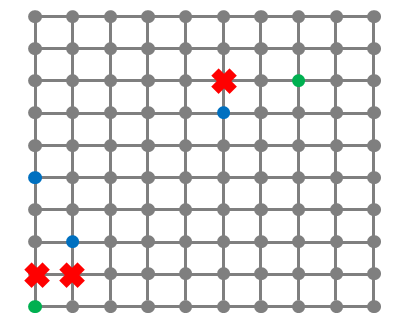
送餐的主要成本体现在路上所花的时间，每一份餐每走一个单位的距离需要花费 \(1\) 块钱。

每个客户的需求都可以由栋栋的任意分店配送，每个分店没有配送总量的限制。

现在你得到了栋栋的客户的需求，请问在最优的送餐方式下，送这些餐需要花费多大的成本。

输入格式

输入的第一行包含四个整数 \(n,m,k,d\)，分别表示方格图的大小、栋栋的分店数量、客户的数量，以及不能经过的点的数量。

接下来 \(m\) 行，每行两个整数 \(x_i,y_i\)

，表示栋栋的一个分店在方格图中的横坐标和纵坐标。

接下来 \(k\) 行，每行三个整数 \(x_i,y_i,c_i\)，分别表示每个客户在方格图中的横坐标、纵坐标和订餐的量。（注意，可能有多个客户在方格图中的同一个位置）

接下来 \(d\) 行，每行两个整数，分别表示每个不能经过的点的横坐标和纵坐标。

输出格式

输出一个整数，表示最优送餐方式下所需要花费的成本。

数据范围

前 \(30%\) 的评测用例满足：\(1≤n≤20\)。

前 \(60%\) 的评测用例满足：\(1≤n≤100\)。

所有评测用例都满足：\(1≤n≤1000,1≤m,k,d≤n^2,1≤x_i,y_i≤n\)。

可能有多个客户在同一个格点上。

每个客户的订餐量不超过 \(1000\)，每个客户所需要的餐都能被送到。

输入样例：

10 2 3 3
1 1
8 8
1 5 1
2 3 3
6 7 2
1 2
2 2
6 8

输出样例：

29

题目分析

\(bfs\) 找到到各点的最短路，计算费用即可

C++ 代码

注： 建议用scanf 读取，不然会\(TLE\)，不然就和我一样关闭流同步

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

typedef pair<int, int> PII;

int dist[N][N] , g[N][N];
pair<PII , int> cus[N * N];
bool st[N][N];
int n , m , k, d;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0) , cout.tie(0);

    cin >> n >> m >> k >> d;
    queue<pair<int , PII>> q;
    while (m -- )
    {
        int x , y;
        cin >> x >> y;
        q.push({0 , {x ,y}});
        st[x][y] = true;
    }

    for(int i = 0 ; i < k ; i ++)
    {
        int x , y , c;
        cin >> x >> y >> c;
        cus[i] = {{x , y} , c};
    }

    while(d --)
    {
        int x , y;
        cin >> x >> y;
        g[x][y] = 1;
    }

    while(q.size())
    {
        auto t = q.front();
        q.pop();
        int dis = t.first , x = t.second.first , y = t.second.second;
        for(int i = 0 ; i < 4 ; i ++)
        {
            int tx = x + dx[i] , ty = y + dy[i];
            if(tx <= 0 || ty <= 0 || tx > n || ty > n || g[tx][ty]) continue;
            if(st[tx][ty]) continue;
            st[tx][ty] = true;
            dist[tx][ty] = dis + 1;
            q.push({dis + 1 , {tx , ty}});
        }
    }

    long long res = 0;
    for(int i = 0 ; i < k ; i ++)
    {
        // cout << dist[cus[i].first.first][cus[i].first.second] << '\n';
        res += dist[cus[i].first.first][cus[i].first.second] * cus[i].second;
    }

    cout << res << '\n';

    return 0;
}