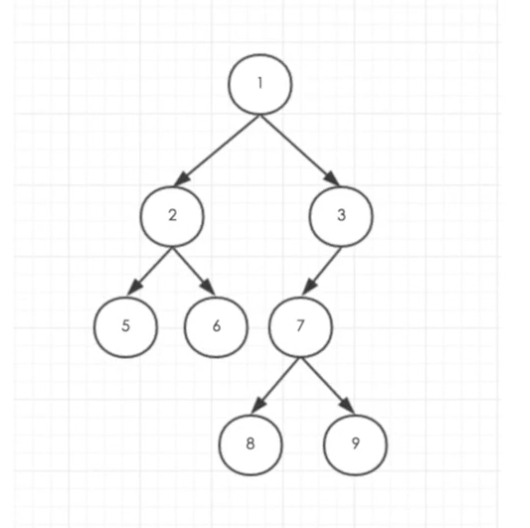
Python实现二叉树的左中右序遍历

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2018/3/18 12:31
# @Author  : baoshan
# @Site    :
# @File    : binarytree.py
# @Software: PyCharm Community Edition

# python 实现二叉树的左中右序遍历

class Node(object):
    def __init__(self, index):
        self.index = index
        self.left_child = None
        self.right_child = None

class BinaryTree(Node):
    def __init__(self, root):
        self.root = root

    def pre_travel(self, node):
        if not node:
            return
        print(node.index)
        self.pre_travel(node.left_child)
        self.pre_travel(node.right_child)

    def mid_travel(self, node):
        if not node:
            return
        self.mid_travel(node.left_child)
        print(node.index)
        self.mid_travel(node.right_child)

    def suf_travel(self, node):
        if not node:
            return
        self.suf_travel(node.left_child)
        self.suf_travel(node.right_child)
        print(node.index)

node_dict = {}
for i in range(1, 10):
    node_dict[i] = Node(i)

node_dict[1].left_child = node_dict[2]
node_dict[1].right_child = node_dict[3]
node_dict[2].left_child = node_dict[5]
node_dict[2].right_child = node_dict[6]
node_dict[3].left_child = node_dict[7]
node_dict[7].left_child = node_dict[8]
node_dict[7].right_child = node_dict[9]

tree = BinaryTree(node_dict[1])
print('---左序遍历---')
tree.pre_travel(tree.root)
print('---中序遍历---')
tree.mid_travel(tree.root)
print('---右序遍历---')
tree.suf_travel(tree.root)

输出结果：

/Library/Frameworks/Python.framework/Versions/3.5/bin/python3.5 /Users/baoshan/PycharmProjects/myProject/python_weixin_study/binarytree.py
---左序遍历---
1
2
5
6
3
7
8
9
---中序遍历---
5
2
6
1
8
7
9
3
---右序遍历---
5
6
2
8
9
7
3
1

Process finished with exit code 0

请各位大虾指教！