多维数组分解----SVD在推荐系统中的应用-

http://www.janscon.com/multiarray/rs_used_svd.html

【声明】本文主要参考自论文《A SINGULAR VALUE DECOMPOSITION APPROACH FOR. RECOMMENDATION SYSTEMS》

1、简介

该文章中提出两个创新点，首先先将User与Item分类，然后根据分类将矩阵分成相应的“子矩阵”，对这些矩阵进行相应的SVD不仅会提高准确率还会降低计算复杂度；另外一个创新点是在于使用<User,Item,tags>三维矩阵，然后通过矩阵分解成<User,Item>、<Item,tags>与<Tags,User>子矩阵后再进行SVD分析，这篇文章的结果表示引入tags会提高推荐性能。

2、用户评分矩阵

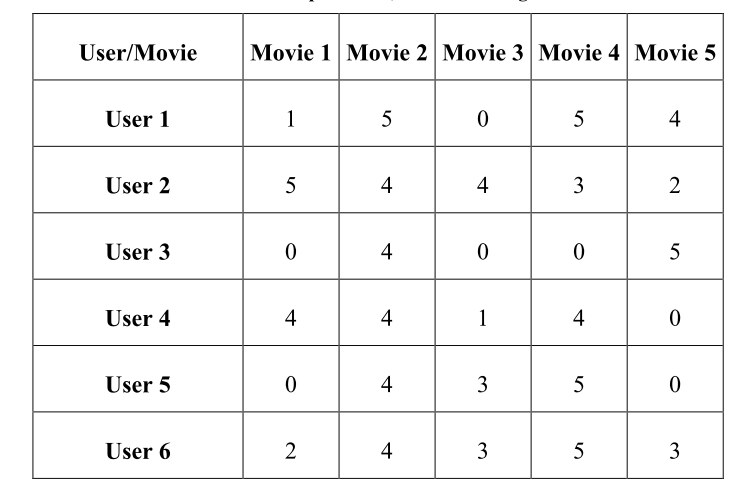评分矩阵

3、进行奇异值分解

使用MATLAB代码：

[U,S,V]=svd(Rating)

得到的数据如下：

U =

-0.4600 0.3964 0.3001 -0.4319 0.3226 -0.5006

-0.4608 -0.3069 -0.6475 0.2837 0.0198 -0.4397

-0.2488 0.7546 -0.2790 0.1563 -0.4646 0.2247

-0.3834 -0.3455 -0.1319 -0.6833 -0.3218 0.3818

-0.3762 -0.2444 0.6212 0.3803 -0.5021 -0.1271

-0.4750 -0.0090 0.0981 0.3115 0.5692 0.5862

S =

16.4664 0 0 0 0

0 6.2100 0 0 0

0 0 4.3991 0 0

0 0 0 2.9034 0

0 0 0 0 1.5845

0 0 0 0 0

V =

-0.3187 -0.4087 -0.7430 -0.3870 0.1721

-0.6120 0.2219 0.0328 -0.1259 -0.7479

-0.2903 -0.3757 -0.1282 0.8703 -0.0260

-0.5752 -0.2556 0.5972 -0.2007 0.4548

-0.3298 0.7598 -0.2717 0.1915 0.4511

至此我们先不管上面的分解结果，在推荐系统中常用的一种做法是先“低秩”逼近，而且常用的是2维逼近。具体做法是：（注意S矩阵中对角线上的奇异值已经按降序排列）取U矩阵的前2列，取S的前2行前2列，取V的前2列：

U(:,1:2),S(1:2,1:2),V(:,1:2)

4、基于User的推荐

使用上面“reduced”过的矩阵进行用户相似度的判定，在推荐系统算法中一步关键的算法是计算用户之间的相似度——一般采用余弦相似度（通过向量内积可计算）或者欧式距离（向量的模值）。

U矩阵中的每一行代表一个用户，两行“距离”越相近表示着两个用户越相似。

=====================================

【问】评分表对应矩阵A，已知 User = x , Item = y , 请问 Rating = ?

① 筛选出所有对Item评过分的用户

② 通过“Reduced“过的矩阵U，找出跟User=x最相近的那个用户

③ 获取最相近的用户对该Item=y的评分，并把这个评分当做User=x对Item=y的评分。

======================================

在第二步中，如果User=x户已经在原来的矩阵A中，按上面步骤计算即可；如果User=x 并不在原来的矩阵A中，这个用户必须要从n维投影到k维（一般是二维）空间中。

如果知道SVD的空间几何意义，理解投影过程就很简单：原来的用户的评分向量(1xn)是在V空间中（n维），将其与Vk矩阵相乘就知道这个用户向量的坐标，然后根据S进行坐标缩放（同时截取前k个值即可），获得的坐标就是用户的评分向量在U空间中的坐标了。

用数学表达的话，设用户向量是，投影到U空间后的向量为P，则有：

然后就可以计算这个用户（用P向量）与其他用户（的各行向量）之间的相似度了。

大量的实验表明，计算相似度的话还是使用欧式距离比较有效。上面的算法瓶颈是如何在“茫茫人海”中找到最相似的那个User。

5、基于Item的推荐

　　使用基于Item的推荐不存在上述的计算瓶颈，因为我们探索的是Item之间的相似度而非User之间的相似度——Item在推荐系统中相对“静态“，变化并不那么明显。因此我们可以离线预先计算好Item直接的相似度，文章《Item-Based Collaborative Filtering Recommendation Algorithms》（Badrul Sarwar等）也指出基于Item的方法在实时效果上要优于基于User的方法。

相类似的，如果要计算两Item之间的相似度需要使用矩阵。每一行代表一个Item，行之间越相近则代表Item之间越相似。其计算过程与上面所讲的User之间的推荐过程很接近。

=====================================

【问题】评分表对应矩阵A，已知 User = x , Item = y , 请问 Rating = ?

① 找出已经被与User=x 评过分的那些Item

② 使用矩阵找出与Item=y最相似的那条Item

③ 获取这最条最相似的Item的评分作为User = x ,Item = y的评分。

=====================================

还是那个问题，第二步中如果Item = y已经存在了，那么之间计算就可以了；如果不存在（也就是说是一条新的Item），就需要投影操作：

设新的Item评分向量是（mx1）,处于U空间（m维），需要投影到V空间（n维）。首先通过内积计算在U空间中的坐标，然后使用Sk反向伸缩坐标即可得到在V空间的坐标。

用数学表达的话，设用户向量是，投影到V空间后的向量为P，则有:

6、增量SVD

　　一般的推荐系统（RS）中，算法是分两步走的：首先是离线训练，之后是在线执行。上两节所讲的是都属于离线计算，一般来讲离线计算都是费事且不频繁。（一般的电影推荐网站，计算User与item表时一天一次甚至一周一次）。

一般的离线SVD对于mxn的矩阵，计算复杂度为，非常费时。一个解决方法是使用“folding-in“，进行增量SVD：

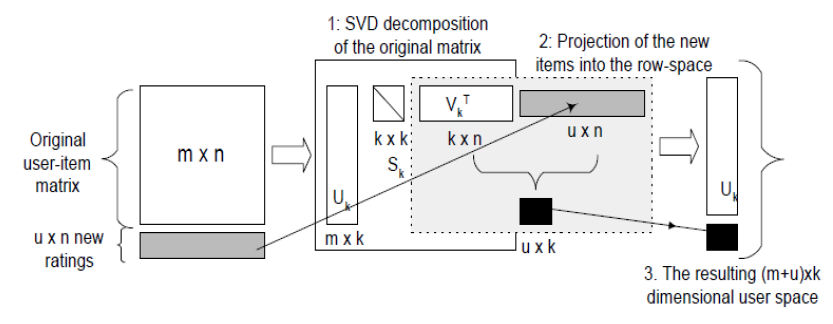
增量的结果是添加进U矩阵。同样的方法可以应用在新Item上。增量SVD的一个直接好处是不会影响之前存在的User（或Item）的坐标，当新用户添加到已经分解的SVD模型中，所付出的时间复杂度是仅仅是O(1)。

（每次离线计算时再全部重新SVD，而线上运行时只进行增量SVD）

7、添加Tags数据

分类之后再逐个分别SVD，明显减少时间。

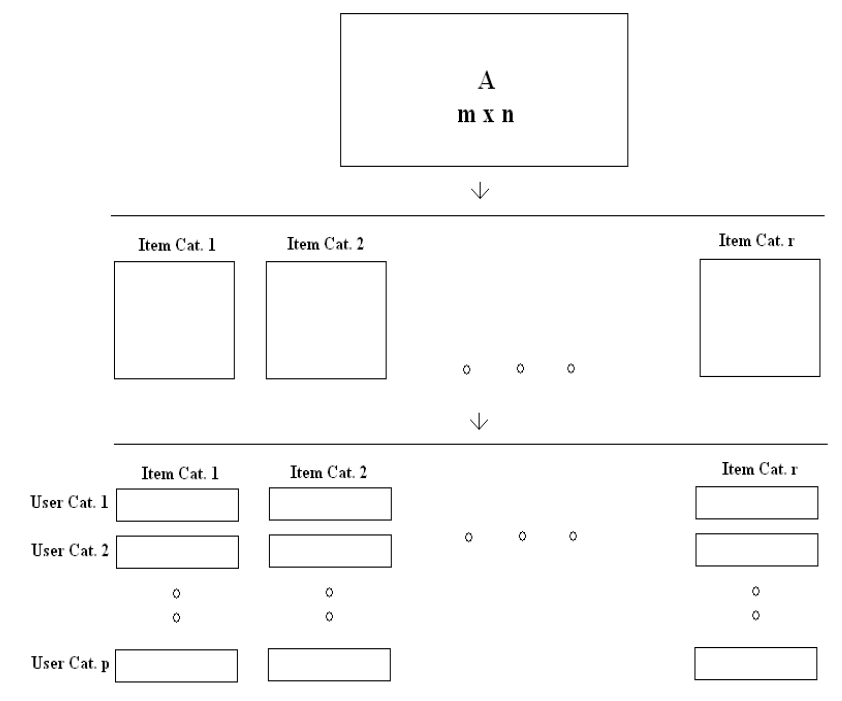
To be Continued…..（未完，有待补充）