poj3335

半平面交&多边形内核。因为没注意了点的情况自闭了。

https://blog.csdn.net/qq_40861916/article/details/83541403

这个说的贼好。

多边形内核就是多边形内部的一块区域/一个点，能看到多边形的任何地方。

怎么求呢。

首先每条边要逆时针。

然后我们对所有的边按照与 +x轴的逆时针夹角进行排序。从小到大。

这之后我们每次用双端队列维护已经求出的多边形。

每加入一条新边的话，我们check一下

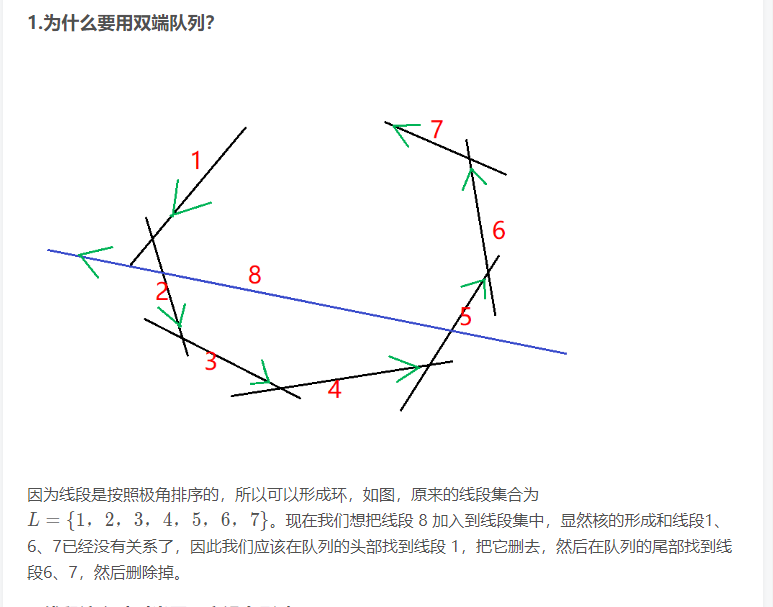
这个图说的太好了！话说这个图的blog我在上面放了链接不算盗用叭。。。

然后就没了。。

 #include <iostream>
 #include <cmath>
 #include <algorithm>
 #include <cstdio>
 #include <vector>
 #include <deque>
 #define rep(x) for(int i=0;i<x;i++)
 using namespace std;
 typedef double db;
 const db eps=1e-;
 const db pi=acos(-);
 int sign(db k){
     if (k>eps) return ; else if (k<-eps) return -; return ;
 }
 int cmp(db k1,db k2){return sign(k1-k2);}
 int inmid(db k1,db k2,db k3){return sign(k1-k3)*sign(k2-k3)<=;}// k3 在 [k1,k2] 内
 struct point{
     db x,y;
     point operator + (const point &k1) const{return (point){k1.x+x,k1.y+y};}
     point operator - (const point &k1) const{return (point){x-k1.x,y-k1.y};}
     point operator * (db k1) const{return (point){x*k1,y*k1};}
     point operator / (db k1) const{return (point){x/k1,y/k1};}
     int operator == (const point &k1) const{return cmp(x,k1.x)==&&cmp(y,k1.y)==;}
     // 逆时针旋转
     point turn(db k1){return (point){x*cos(k1)-y*sin(k1),x*sin(k1)+y*cos(k1)};}
     point turn90(){return (point){-y,x};}
     bool operator < (const point k1) const{
         int a=cmp(x,k1.x);
         if (a==-) return ; else if (a==) return ; else return cmp(y,k1.y)==-;
     }
     db abs(){return sqrt(x*x+y*y);}
     db abs2(){return x*x+y*y;}
     db dis(point k1){return ((*this)-k1).abs();}
     point unit(){db w=abs(); return (point){x/w,y/w};}
     void scan(){double k1,k2; scanf("%lf%lf",&k1,&k2); x=k1; y=k2;}
     void print(){printf("%.11lf %.11lf\n",x,y);}
     db getw(){return atan2(y,x);}
     point getdel(){if (sign(x)==-||(sign(x)==&&sign(y)==-)) return (*this)*(-); else return (*this);}
     int getP() const{return sign(y)==||(sign(y)==&&sign(x)==-);}
 };
 int inmid(point k1,point k2,point k3){return inmid(k1.x,k2.x,k3.x)&&inmid(k1.y,k2.y,k3.y);}
 db cross(point k1,point k2){return k1.x*k2.y-k1.y*k2.x;}
 db dot(point k1,point k2){return k1.x*k2.x+k1.y*k2.y;}
 db rad(point k1,point k2){return atan2(cross(k1,k2),dot(k1,k2));}
 // -pi -> pi
 int compareangle (point k1,point k2){
     return k1.getP()<k2.getP()||(k1.getP()==k2.getP()&&sign(cross(k1,k2))>);
 }
 point proj(point k1,point k2,point q){ // q 到直线 k1,k2 的投影
     point k=k2-k1; return k1+k*(dot(q-k1,k)/k.abs2());
 }
 point reflect(point k1,point k2,point q){return proj(k1,k2,q)*-q;}
 int clockwise(point k1,point k2,point k3){// k1 k2 k3 逆时针 1 顺时针 -1 否则 0
     return sign(cross(k2-k1,k3-k1));
 }
 int checkLL(point k1,point k2,point k3,point k4){// 求直线 (L) 线段 (S)k1,k2 和 k3,k4 的交点
     return cmp(cross(k3-k1,k4-k1),cross(k3-k2,k4-k2))!=;
 }
 point getLL(point k1,point k2,point k3,point k4){
     db w1=cross(k1-k3,k4-k3),w2=cross(k4-k3,k2-k3); return (k1*w2+k2*w1)/(w1+w2);
 }
 int intersect(db l1,db r1,db l2,db r2){
     if (l1>r1) swap(l1,r1); if (l2>r2) swap(l2,r2); return cmp(r1,l2)!=-&&cmp(r2,l1)!=-;
 }
 int checkSS(point k1,point k2,point k3,point k4){
     return intersect(k1.x,k2.x,k3.x,k4.x)&&intersect(k1.y,k2.y,k3.y,k4.y)&&
            sign(cross(k3-k1,k4-k1))*sign(cross(k3-k2,k4-k2))<=&&
            sign(cross(k1-k3,k2-k3))*sign(cross(k1-k4,k2-k4))<=;
 }
 db disSP(point k1,point k2,point q){
     point k3=proj(k1,k2,q);
     if (inmid(k1,k2,k3)) return q.dis(k3); else return min(q.dis(k1),q.dis(k2));
 }
 db disSS(point k1,point k2,point k3,point k4){
     if (checkSS(k1,k2,k3,k4)) return ;
     else return min(min(disSP(k1,k2,k3),disSP(k1,k2,k4)),min(disSP(k3,k4,k1),disSP(k3,k4,k2)));
 }
 int onS(point k1,point k2,point q){return inmid(k1,k2,q)&&sign(cross(k1-q,k2-k1))==;}
 struct circle{
     point o; db r;
     void scan(){o.scan(); scanf("%lf",&r);}
     int inside(point k){return cmp(r,o.dis(k));}
 };
 struct line{
     // p[0]->p[1]
     point p[];
     line(point k1,point k2){p[]=k1; p[]=k2;}
     point& operator [] (int k){return p[k];}
     int include(point k){return sign(cross(p[]-p[],k-p[]))>=;}//非严格包含。
     point dir(){return p[]-p[];}
     line push(){ // 向外 ( 左手边 ) 平移 eps
         const db eps = 1e-;
         point delta=(p[]-p[]).turn90().unit()*eps;
         return {p[]-delta,p[]-delta};
     }
 };
 point getLL(line k1,line k2){return getLL(k1[],k1[],k2[],k2[]);}
 int parallel(line k1,line k2){return sign(cross(k1.dir(),k2.dir()))==;}
 int sameDir(line k1,line k2){return parallel(k1,k2)&&sign(dot(k1.dir(),k2.dir()))==;}
 int operator < (line k1,line k2){
     if (sameDir(k1,k2)) return k2.include(k1[]);
     return compareangle(k1.dir(),k2.dir());
 }
 int checkpos(line k1,line k2,line k3){return k3.include(getLL(k1,k2));}
 vector<line> getHL(vector<line> &L){ // 求半平面交 , 半平面是逆时针方向 , 输出按照逆时针
     sort(L.begin(),L.end()); deque<line> q;
     for (int i=;i<(int)L.size();i++){
         if (i&&sameDir(L[i],L[i-])) continue;
         while (q.size()>&&!checkpos(q[q.size()-],q[q.size()-],L[i])) q.pop_back();
         while (q.size()>&&!checkpos(q[],q[],L[i])) q.pop_front();
         q.push_back(L[i]);
     }
     while (q.size()>&&!checkpos(q[q.size()-],q[q.size()-],q[])) q.pop_back();
     while (q.size()>&&!checkpos(q[],q[],q[q.size()-])) q.pop_front();
     vector<line>ans; for (int i=;i<q.size();i++) ans.push_back(q[i]);
     return ans;
 }
 int t,n;
 point p[];
 bool cw(){//时针
     db s=;
     for(int i=;i<n-;i++){
         s+=cross(p[i]-p[],p[i+]-p[]);
     }
     return s>;
 }
 vector<line> l;
 int main(){
     scanf("%d",&t);
     while (t--){
         scanf("%d",&n);
         rep(n) scanf("%lf%lf",&p[i].x,&p[i].y);
         if(!cw())reverse(p,p+n);
         for(int i=;i<n;i++){
             l.push_back(line(p[i],p[(i+)%n]));
         }
         l=getHL(l);
         if(l.size()>=){
             printf("YES\n");
         } else{
             printf("NO\n");
         }
         l.clear();
     }
 }
 /**
 1
 17
 2 -1  2 -2  1 -2  0 -1  -1 -2  -2 -2  -2 -1  -1 0  -2 1  -2 2  -1 2  0 1  1 2  3 2  3 1  2 1  1 0

 */