Minimum Domino Rotations For Equal Row LT1007

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the i-th domino.  (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i-th domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

Example 1:

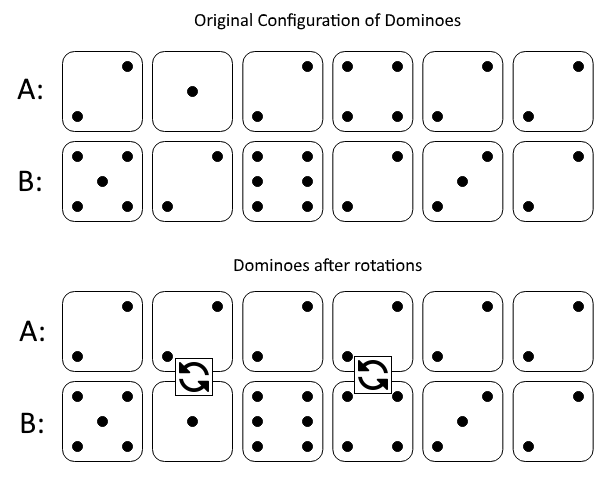
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Idea 1. Bruteforce, swap or not swap(0-1), similar to subsets problem, typical backtracking

Time complexity: O(n2^n)

Space complexity: O(1)

 class Solution {
     private void swap(int[] A, int[] B, int pos) {
         int temp = A[pos];
         A[pos] = B[pos];
         B[pos] = temp;
     }
     private boolean isEqual(int[] A) {
         for(int i = 1; i < A.length; ++i) {
             if(A[i] != A[i-1]) {
                 return false;
             }
         }
         return true;
     }

     private void helper(int[] A, int[] B, int pos, int currCnt, int[] cnt) {
         if(pos == A.length) {
             if(isEqual(A) || isEqual(B)) {
                 cnt[0] = Math.min(cnt[0], currCnt);
             }
             return;
         }

         if(A[pos] != B[pos]) {
             swap(A, B, pos);
             helper(A, B, pos+1, currCnt+1, cnt);
             swap(A, B, pos);
         }

         helper(A, B, pos+1, currCnt, cnt);
     }
     public int minDominoRotations(int[] A, int[] B) {
         int[] cnt = new int[1];
         cnt[0] = Integer.MAX_VALUE;
         helper(A, B, 0, 0, cnt);
         return cnt[0] == Integer.MAX_VALUE? -1: cnt[0];
     }
 }

Idea 2. 有时候具体的题目要求更restrict, 反而简化了问题，这题要求all elments equal in A[i] or B[i], 如果我们知道交换后的结果数组的相同数，只能是四种：A-> { A[0], B[0] }, B-> { A[0], B[0] },

make A be all A[0] or B[0]

make B be all A[0] or B[0]

然后计算最小步数

Time complexity: O(n), 4 times scan

Space complexity: O(1)

 class Solution {
     int helper(int[] A, int[] B, int target) {
         int cnt = 0;
         for(int i = 0; i < A.length; ++i) {
             if(A[i] != target) {
                 if(B[i] == target) {
                     ++cnt;
                 }
                 else {
                     return Integer.MAX_VALUE;
                 }
             }
         }
         return cnt;
     }
     public int minDominoRotations(int[] A, int[] B) {
            int result = Math.min(helper(A, B, A[0]),
                                  helper(A, B, B[0]));
            result = Math.min(result,
                              Math.min(helper(B,A, B[0]),
                                      helper(B, A, A[0])));
            return result == Integer.MAX_VALUE? -1: result;
     }
 }

Idea 2.a 网上看到的，一次遍历同时计算A,B所需的步数

Time complexity: O(n), 2 times scan

Space comlexity: O(1)

 class Solution {
     private int helper(int[] A, int[] B, int target) {
         int swapA = 0, swapB = 0;
         for(int i = 0; i < A.length; ++i) {
             if(A[i] != target && B[i] != target) {
                 return Integer.MAX_VALUE;
             }

             if(A[i] != target){
                 ++swapA;
             }
             else if(B[i] != target) {
                 ++swapB;
             }
         }

         return Math.min(swapA, swapB);
     }
     public int minDominoRotations(int[] A, int[] B) {
            int result = Math.min(helper(A, B, A[0]),
                                 helper(A, B, B[0]));

            return result == Integer.MAX_VALUE? -1: result;
     }
 }

Idea 3. intersection set of {A{i}, B{i}}, 为了完成swap可以让数组相等，each position in either A or B should have the element, we can use set.retailAll, the steps = A.length - countA[A[i]]

Time complexity: O(n)

Space complexity: O(1), HashMap + HashSet

 class Solution {
     public int minDominoRotations(int[] A, int[] B) {
           Set<Integer> candidates = new HashSet<>(Arrays.asList(1, 2, 3, 4, 5, 6));
           int[] countA = new int[7];
           int[] countB = new int[7];

           for(int i = 0; i < A.length; ++i) {
               ++countA[A[i]];
               ++countB[B[i]];
               candidates.retainAll(new HashSet<>(Arrays.asList(A[i], B[i])));
           }

            for(int val: candidates) {
                return Math.min(A.length - countA[val], A.length - countB[val]);
            }

            return -1;
     }
 }

用数组代表set

 class Solution {
     public int minDominoRotations(int[] A, int[] B) {
           int[] countA = new int[7];
           int[] countB = new int[7];
           int[] common = new int[7];

           for(int i = 0; i < A.length; ++i) {
               ++countA[A[i]];
               ++countB[B[i]];
               if(A[i] == B[i]) {
                   ++common[A[i]];
               }
           }

           for(int i = 1; i < 7; ++i) {
               if(countA[i] + countB[i] - common[i] >= A.length) {
                   return Math.min(A.length - countA[i], A.length - countB[i]);
               }
           }

            return -1;
     }
 }