P4841 城市规划 FFT+生成函数

\(\color{#0066ff}{ 题目描述 }\)

刚刚解决完电力网络的问题, 阿狸又被领导的任务给难住了. 刚才说过, 阿狸的国家有n个城市, 现在国家需要在某些城市对之间建立一些贸易路线, 使得整个国家的任意两个城市都直接或间接的连通. 为了省钱, 每两个城市之间最多只能有一条直接的贸易路径. 对于两个建立路线的方案, 如果存在一个城市对, 在两个方案中是否建立路线不一样, 那么这两个方案就是不同的, 否则就是相同的. 现在你需要求出一共有多少不同的方案. 好了, 这就是困扰阿狸的问题. 换句话说, 你需要求出n个点的简单(无重边无自环)无向连通图数目. 由于这个数字可能非常大, 你只需要输出方案数mod 1004535809(479 * 2 ^ 21 + 1)即可.

\(\color{#0066ff}{输入格式}\)

一行，四个整数，N、M、x、|S|，其中|S|为集合S中元素个数。第二行，|S|个整数，表示集合S中的所有元素。

\(\color{#0066ff}{输出格式}\)

一行，一个整数，表示你求出的种类数mod 1004535809的值。

\(\color{#0066ff}{输入样例}\)

3

4

100000

\(\color{#0066ff}{输出样例}\)

4

38

829847355

\(\color{#0066ff}{数据范围与提示}\)

对于 20%的数据, n <= 10

对于 40%的数据, n <= 1000

对于 60%的数据, n <= 30000

对于 80%的数据, n <= 60000

对于 100%的数据, n <= 130000

\(\color{#0066ff}{ 题解 }\)

直接构造出g，求个ln（指数生成函数）

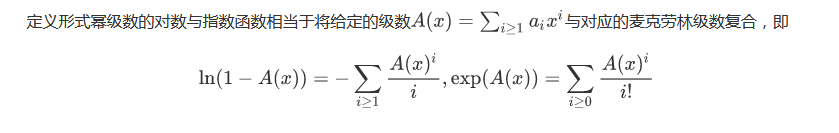
最初系数/i!是好算，最后要乘回来

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
using std::vector;
const int maxn = 1e6 + 20;
const int mod = 1004535809;
int len, r[maxn];
LL ksm(LL x, LL y) {
	LL re = 1LL;
	while(y) {
		if(y & 1) re = re * x % mod;
		x = x * x % mod;
		y >>= 1;
	}
	return re;
}
void FNTT(vector<int> &A, int flag) {
	A.resize(len);
	for(int i = 0; i < len; i++) if(i < r[i]) std::swap(A[i], A[r[i]]);
	for(int l = 1; l < len; l <<= 1) {
		int w0 = ksm(3, (mod - 1) / (l << 1));
		for(int i = 0; i < len; i += (l << 1)) {
			int w = 1, a0 = i, a1 = i + l;
			for(int k = 0; k < l; k++, a0++, a1++, w = 1LL * w0 * w % mod) {
				int tmp = 1LL * A[a1] * w % mod;
				A[a1] = ((A[a0] - tmp) % mod + mod) % mod;
				A[a0] = (A[a0] + tmp) % mod;
			}
		}
	}
	if(!(~flag)) {
		std::reverse(A.begin() + 1, A.end());
		int inv = ksm(len, mod - 2);
		for(int i = 0; i < len; i++) A[i] = 1LL * A[i] * inv % mod;
	}
}
vector<int> operator * (vector<int> A, vector<int> B) {
	int tot = A.size() + B.size() - 1;
	for(len = 1; len <= tot; len <<= 1);
	for(int i = 0; i < len; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) * (len >> 1));
	FNTT(A, 1), FNTT(B, 1);
	vector<int> ans;
	for(int i = 0; i < len; i++) ans.push_back(1LL * A[i] * B[i] % mod);
	FNTT(ans, -1);
	ans.resize(tot);
	return ans;
}
vector<int> operator - (const vector<int> &A, const vector<int> &B) {
	vector<int> ans;
	for(int i = 0; i < (int)std::min(A.size(), B.size()); i++) ans.push_back(A[i] - B[i]);
	for(int i = B.size(); i < (int)A.size(); i++) ans.push_back(A[i]);
	for(int i = A.size(); i < (int)B.size(); i++) ans.push_back(-B[i]);
	return ans;
}
vector<int> inv(const vector<int> &A) {
	if(A.size() == 1) {
		vector<int> ans;
		ans.push_back(ksm(A[0], mod - 2));
		return ans;
	}
	int n = A.size(), _ = (n + 1) >> 1;
	vector<int> B = A, ans;
	B.resize(_);
	B = inv(B);
	ans.push_back(2);
	ans = B * (ans - A * B);
	ans.resize(n);
	return ans;
}
vector<int> getd(const vector<int> &A) {
	vector<int> ans;
	ans.resize(A.size() - 1);
	for(int i = 1; i < (int)A.size(); i++) ans[i - 1] = 1LL * i * A[i] % mod;
	return ans;
}
vector<int> geti(const vector<int> &A) {
	vector<int> ans;
	ans.resize(A.size() + 1);
	for(int i = 1; i < (int)ans.size(); i++) ans[i] = 1LL * A[i - 1] * ksm(i, mod - 2) % mod;
	return ans;
}
vector<int> ln(const vector<int> &A) {
	vector<int> B = getd(A), C = inv(A);
	return geti(B * C);
}
int main() {
	int n = in();
	vector<int> a;
	static int fac[maxn];
	fac[0] = 1;
	for(int i = 1; i <= n; i++) fac[i] = 1LL * fac[i - 1] * i % mod;
	for(int i = 0; i <= n; i++) a.push_back(1LL * ksm(2, (((LL)i * (i - 1)) / 2)) * ksm(fac[i], mod - 2) % mod);
	a = ln(a);
	printf("%d\n", (int)(1LL * a[n] * fac[n] % mod));
	return 0;

}