四边形不等式优化DP——石子合并问题 学习笔记

好方啊马上就要区域赛了连DP都不会QAQ

毛子青《动态规划算法的优化技巧》论文里面提到了一类问题：石子合并。

n堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。

求出将n堆石子合并成一堆的最小得分和最大得分以及相应的合并方案。

设m[i,j]表示合并d[i..j]所得到的最小得分。

状态转移方程：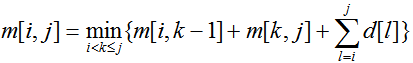

总的时间复杂度为O(n³）。

【优化方案】

四边形不等式：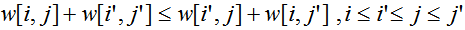

m[i,j]满足四边形不等式

令s[i,j]=max{k | m[i,j]=m[i,k-1]+m[k,j]+w[i,j] }

m[i,j]满足四边形不等式可以推出函数s[i,j]的单调性，即s[i,j]≤s[i,j+1]≤s[i+1,j+1],     i≤j

优化的状态转移方程：

状态转移方程 m[i][j]=min{m[i][k-1]+m[k][j]}+w[i][j]}  (i<=k<=j)

如果w同时满足四边形不等式和区间单调关系，则m也满足四边形不等式

四边形不等式优化的作用：m满足四边形不等式 -> k最优决策单调性

参考博客：http://blog.csdn.net/bnmjmz/article/details/41308919

  #include <string.h>
#include <iostream>
#include <list>
#include <map>
#include <set>
#include <stack>
#include <string>
#include <utility>
#include <vector>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#define  LL long long
#define MOD 1000000007

using namespace std;

const int INF = 0x3f3f3f;
const int N = ;

int m[N][N]; //m[i,j]表示合并d[i..j]所得到的最小得分
int s[N][N];  //s[i,j]记录合并方案
int sum[N]; //前i个石子堆石子数量和
int n;

int solve()
{
    for(int i=; i<=n; i++)
    {
        m[i][i] = ;   //边界条件
        s[i][i] = i;
    }
        for(int l=; l<n; l++)  //枚举 l = j' - i
        {
            for(int i=; i+l<=n; i++)
            {
                int j = i+l;
                int tmp = INF;
                int k = ;
                for(int div=s[i][j-]; div<=s[i+][j];div++) //最优决策的单调性
                {
                    if(tmp > m[i][div] + m[div+][j] + sum[j] - sum[i-] )
                    {
                        tmp = m[i][div] + m[div+][j] + sum[j] - sum[i-];
                        k = div;
                    }
                }
                m[i][j] = tmp;
                s[i][j] = k;
            }
        }
        return m[][n];
}

int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        sum[] = ;
        for(int i=; i<=n; i++)
        {
            int a;
            scanf("%d",&a);
            sum[i] = sum[i-] + a;
        }
        printf("%d\n",solve());
    }
    return ;
}