Floyd算法(二)之 C++详解

本章是弗洛伊德算法的C++实现。

目录
1. 弗洛伊德算法介绍
2. 弗洛伊德算法图解
3. 弗洛伊德算法的代码说明
4. 弗洛伊德算法的源码

转载请注明出处：http://www.cnblogs.com/skywang12345/

更多内容：数据结构与算法系列 目录

弗洛伊德算法介绍

和Dijkstra算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

基本思想

通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入一个矩阵S，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

假设图G中顶点个数为N，则需要对矩阵S进行N次更新。初始时，矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞。 接下来开始，对矩阵S进行N次更新。第1次更新时，如果"a[i][j]的距离" > "a[i][0]+a[0][j]"(a[i][0]+a[0][j]表示"i与j之间经过第1个顶点的距离")，则更新a[i][j]为"a[i][0]+a[0][j]"。 同理，第k次更新时，如果"a[i][j]的距离" > "a[i][k]+a[k][j]"，则更新a[i][j]为"a[i][k]+a[k][j]"。更新N次之后，操作完成！

单纯的看上面的理论可能比较难以理解，下面通过实例来对该算法进行说明。

弗洛伊德算法图解

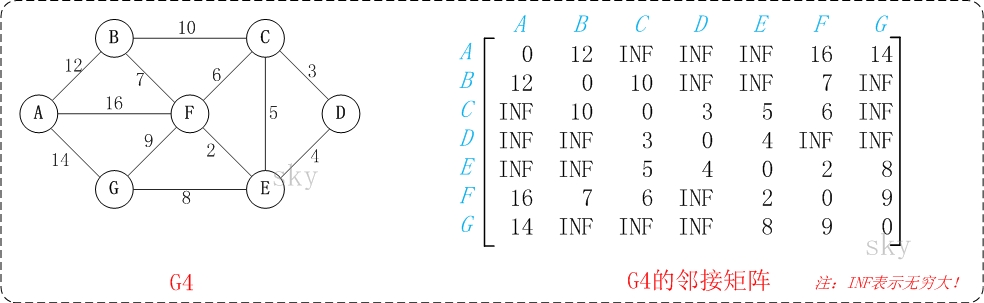
以上图G4为例，来对弗洛伊德进行算法演示。

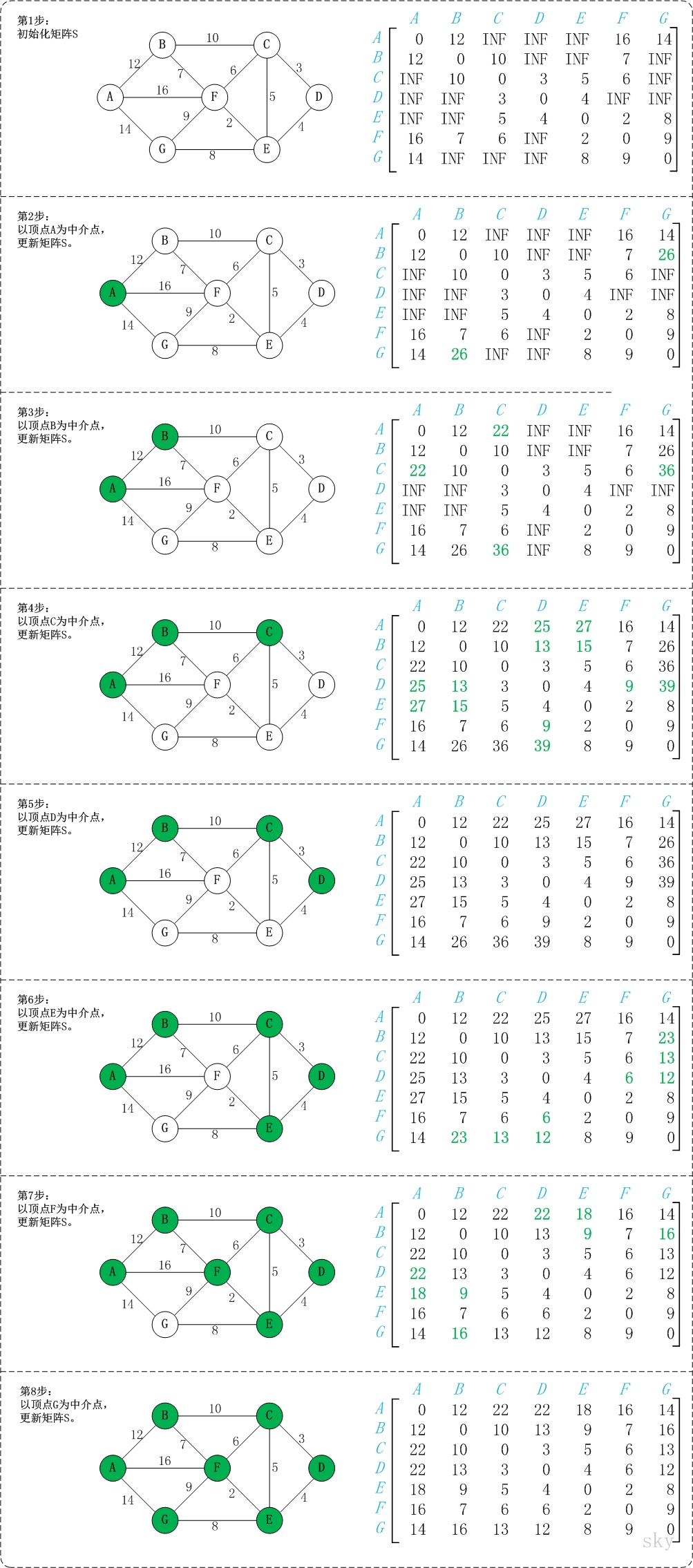
初始状态：S是记录各个顶点间最短路径的矩阵。
第1步：初始化S。
    矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞。实际上，就是将图的原始矩阵复制到S中。
    注:a[i][j]表示矩阵S中顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

第2步：以顶点A(第1个顶点)为中介点，若a[i][j] > a[i][0]+a[0][j]，则设置a[i][j]=a[i][0]+a[0][j]。
    以顶点a[1]6，上一步操作之后，a[1][6]=∞；而将A作为中介点时，(B,A)=12，(A,G)=14，因此B和G之间的距离可以更新为26。

同理，依次将顶点B,C,D,E,F,G作为中介点，并更新a[i][j]的大小。

弗洛伊德算法的代码说明

以"邻接矩阵"为例对弗洛伊德算法进行说明，对于"邻接表"实现的图在后面会给出相应的源码。

1. 基本定义

class MatrixUDG {
    #define MAX    100
    #define INF    (~(0x1<<31))        // 无穷大(即0X7FFFFFFF)
    private:
        char mVexs[MAX];    // 顶点集合
        int mVexNum;             // 顶点数
        int mEdgNum;             // 边数
        int mMatrix[MAX][MAX];   // 邻接矩阵

    public:
        // 创建图(自己输入数据)
        MatrixUDG();
        // 创建图(用已提供的矩阵)
        //MatrixUDG(char vexs[], int vlen, char edges[][2], int elen);
        MatrixUDG(char vexs[], int vlen, int matrix[][9]);
        ~MatrixUDG();

        // 深度优先搜索遍历图
        void DFS();
        // 广度优先搜索（类似于树的层次遍历）
        void BFS();
        // prim最小生成树(从start开始生成最小生成树)
        void prim(int start);
        // 克鲁斯卡尔（Kruskal)最小生成树
        void kruskal();
        // Dijkstra最短路径
        void dijkstra(int vs, int vexs[], int dist[]);
        // Floyd最短路径
        void floyd(int path[][MAX], int dist[][MAX]);
        // 打印矩阵队列图
        void print();

    private:
        // 读取一个输入字符
        char readChar();
        // 返回ch在mMatrix矩阵中的位置
        int getPosition(char ch);
        // 返回顶点v的第一个邻接顶点的索引，失败则返回-1
        int firstVertex(int v);
        // 返回顶点v相对于w的下一个邻接顶点的索引，失败则返回-1
        int nextVertex(int v, int w);
        // 深度优先搜索遍历图的递归实现
        void DFS(int i, int *visited);
        // 获取图中的边
        EData* getEdges();
        // 对边按照权值大小进行排序(由小到大)
        void sortEdges(EData* edges, int elen);
        // 获取i的终点
        int getEnd(int vends[], int i);
};

Graph是邻接矩阵对应的结构体。
vexs用于保存顶点，vexnum是顶点数，edgnum是边数；matrix则是用于保存矩阵信息的二维数组。例如，matrix[i][j]=1，则表示"顶点i(即vexs[i])"和"顶点j(即vexs[j])"是邻接点；matrix[i][j]=0，则表示它们不是邻接点。

2. 弗洛伊德算法

/*
 * floyd最短路径。
 * 即，统计图中各个顶点间的最短路径。
 *
 * 参数说明：
 *     path -- 路径。path[i][j]=k表示，"顶点i"到"顶点j"的最短路径会经过顶点k。
 *     dist -- 长度数组。即，dist[i][j]=sum表示，"顶点i"到"顶点j"的最短路径的长度是sum。
 */
void MatrixUDG::floyd(int path[][MAX], int dist[][MAX])
{
    int i,j,k;
    int tmp;

    // 初始化
    for (i = 0; i < mVexNum; i++)
    {
        for (j = 0; j < mVexNum; j++)
        {
            dist[i][j] = mMatrix[i][j];    // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
            path[i][j] = j;                // "顶点i"到"顶点j"的最短路径是经过顶点j。
        }
    }

    // 计算最短路径
    for (k = 0; k < mVexNum; k++)
    {
        for (i = 0; i < mVexNum; i++)
        {
            for (j = 0; j < mVexNum; j++)
            {
                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp)
                {
                    // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                    dist[i][j] = tmp;
                    // "i到j最短路径"对应的路径，经过k
                    path[i][j] = path[i][k];
                }
            }
        }
    }

    // 打印floyd最短路径的结果
    cout << "floyd: " << endl;
    for (i = 0; i < mVexNum; i++)
    {
        for (j = 0; j < mVexNum; j++)
            cout << setw(2) << dist[i][j] << "  ";
        cout << endl;
    }
}

弗洛伊德算法的源码

这里分别给出"邻接矩阵图"和"邻接表图"的弗洛伊德算法源码。

1. 邻接矩阵源码(MatrixUDG.cpp)

2. 邻接表源码(ListUDG.cpp)